お疲れ様でした。
| 日付 | 曜日 | 開始〜終了 | 作業時間 | 立合 | 作業内容 |
| 4/18 | 月曜 | 16:00~16:30 | 0.5 | 後藤 | ログインアウト |
| 4/25 | 月曜 | 16:00~17:00 | 1.0 | 後藤 | vi編集 |
| 5/5 | 木曜 | 16:30~17:30 | 1.0 | 後藤 | 課題作成 vi面積 |
| 5/9 | 月曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 vi最大最小 |
| 5/16 | 月曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 ccx片持ち梁 |
| 5/17 | 火曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 ccx片持ち梁 |
| 5/19 | 木曜 | 15:00~16:30 | 1.5 | 後藤 | 課題作成 ccx片持ち梁 |
| 5/23 | 月曜 | 16:00~19:00 | 3.0 | 後藤 | 課題作成 ccx片持ち梁 |
| 5/26 | 木曜 | 15:30~16:30 | 1.0 | 後藤 | 課題作成 ネットに貼り付け |
| 6/2 | 木曜 | 14:30~16:00 | 1.5 | 後藤 | 課題作成 ccx片持ち梁 |
| 6/13 | 月曜 | 16:30~18:00 | 1.5 | 後藤 | 課題作成 ティモシェンコ梁 |
| 6/16 | 木曜 | 16:30~18:00 | 1.5 | 後藤 | 課題作成 ティモシェンコ梁 |
| 6/30 | 木曜 | 14:30~16:00 | 1.5 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁) |
| 7/1 | 金曜 | 20:00~22:00 | 2.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁) |
| 7/2 | 土曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁) |
| 7/7 | 木曜 | 15:30~16:30 | 1.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 7/8 | 金曜 | 18:30~19:30 | 1.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 7/28 | 木曜 | 07:40~17:40 | 10.0 | 後藤 | 試験橋の架設 |
| 7/29 | 金曜 | 07:40~17:40 | 10.0 | 後藤 | 試験橋の架設 |
| 8/1 | 月曜 | 17:00~18:00 | 1.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 8/2 | 火曜 | 13:00~16:00 | 3.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 8/3 | 水曜 | 16:00~19:00 | 3.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 8/5 | 金曜 | 14:00~20:30 | 6.0 | 後藤 | 課題作成 たわみの比較(有限要素、初等梁、ティモシェンコ梁)直交異方性 |
| 8/8 | 月曜 | 千田 | 合宿 | ||
| 8/9 | 火曜 | 千田 | 合宿 | ||
| 8/10 | 水曜 | 千田 | 合宿 | ||
| 9/15 | 木曜 | 16:00~17:00 | 1.0 | 後藤 | データ整理 |
| 9/25 | 日曜 | 10:00~13:00 | 3.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 9/27 | 火曜 | 10:00~15:00 | 4.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 9/28 | 水曜 | 16:00~18:30 | 2.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 9/29 | 木曜 | 20:00~22:00 | 2.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/1 | 土曜 | 15:00~18:00 | 3.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/4 | 火曜 | 19:00~24:00 | 5.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/5 | 水曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/8 | 土曜 | 14:00~21:00 | 6.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/11 | 火曜 | 16:30~19:30 | 3.0 | 後藤 | 課題作成 直交異方性でのGを求める latex |
| 10/12 | 水曜 | 12:00~20:30 | 4.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/13 | 木曜 | 12:30~19:00 | 4.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/14 | 金曜 | 16:30~21:00 | 4.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/16 | 日曜 | 13:00~17:30 | 2.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/17 | 月曜 | 14:00~19:30 | 5.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/18 | 火曜 | 16:30~20:00 | 3.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 10/19 | 水曜 | 13:00~18:00 | 3.0 | 後藤 | オープンキャンパス準備 |
| 10/21 | 金曜 | 17:00~22:00 | 3.0 | 後藤 | 課題作成 直交異方性でのGを求める latex |
| 10/24 | 月曜 | 15:30~17:00 | 1.5 | 後藤 | 課題作成 直交異方性でのGを求める latex |
| 10/26 | 水曜 | 10:30~16:00 | 3.0 | 後藤 | 課題作成 直交異方性でのGを求める latex |
| 10/28 | 金曜 | 16:30~19:30 | 2.0 | 後藤 | 課題作成 直交異方性でのGを求める latex |
| 11/7 | 月曜 | 16:00~22:00 | 5.0 | 後藤 | 課題作成 直交異方性でのGを求める |
| 11/8 | 火曜 | 17:00~20:30 | 3.5 | 後藤 | 課題作成 直交異方性でのGを求める |
| 11/9 | 水曜 | 10:30~12:30 | 1.5 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/17 | 木曜 | 19:30~22:30 | 3.0 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/18 | 金曜 | 16:00~18:00 | 2.0 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/22 | 火曜 | 19:30~22:00 | 2.5 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/24 | 木曜 | 18:00~19:00 | 1.0 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/28 | 月曜 | 19:30~25:00 | 5.0 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/29 | 火曜 | 20:30~24:30 | 4.0 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 11/30 | 水曜 | 11:00~18:00 | 5.5 | 後藤 | 課題作成 両端支持のプログラム作成 |
| 12/1 | 木曜 | 15:30~18:30 | 3.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/4 | 日曜 | 17:00~20:00 | 3.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/5 | 月曜 | 15:00~20:30 | 5.5 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/6 | 火曜 | 17:00~20:30 | 3.5 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/7 | 水曜 | 10:30~20:00 | 8.5 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/9 | 金曜 | 15:00~22:00 | 7.5 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/12 | 月曜 | 18:00~22:00 | 4.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/13 | 火曜 | 18:00~24:00 | 6.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/14 | 水曜 | 11:00~25:30 | 11.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/15 | 木曜 | 19:00~26:30 | 6.0 | 後藤 | 課題作成 スライド作成 |
| 12/16 | 金曜 | 13:00~22:30 | 6.0 | 後藤 | 課題作成 スライド作成 |
| 12/17 | 土曜 | 23:00~11:00 | 9.0 | 後藤 | 課題作成 スライド作成 |
| 12/19 | 月曜 | 後藤 | 中間発表 | ||
| 12/20 | 火曜 | 20:00~27:00 | 7.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/23 | 金曜 | 13:00~22:30 | 5.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 12/30 | 金曜 | 13:00~16:00 | 3.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 1/10 | 火曜 | 16:00~21:30 | 2.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 1/17 | 火曜 | 15:00~22:00 | 6.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 1/18 | 水曜 | 10:30~24:00 | 12.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 1/19-20 | 木金 | 20:00~20:30 | 20.0 | 後藤 | 課題作成 両端支持のプログラム作成 確認 |
| 1/21-22 | 土日 | 02:00~17:00 | 12.0 | 後藤 | 課題作成 TEX |
| 1/23 | 月曜 | 17:00~28:00 | 10.0 | 後藤 | 課題作成 TEX |
| 1/24 | 火曜 | 15:00~25:00 | 8.0 | 後藤 | 課題作成 TEX |
| 1/25 | 水曜 | 11:00~16:00 | 4.0 | 後藤 | 課題作成 TEX |
| 1/28 | 土曜 | 17:00~19:00 | 2.0 | 後藤 | 課題作成 スライド |
| 1/30 | 月曜 | 12:00~22:00 | 7.0 | 後藤 | 課題作成 スライド 解析 |
| 1/31 | 火曜 | 16:30~25:30 | 6.0 | 後藤 | 課題作成 スライド 解析 |
| 2/1-2 | 水木 | 13:30~16:30 | 20.0 | 後藤 | 課題作成 スライド |
| 2/3 | 金曜 | 14:00~16:00 | 2.0 | 後藤 | 課題作成 スライド |
| 2/6 | 月曜 | 14:00~28:00 | 10.0 | 後藤 | 課題作成 スライド |
| 合計 | 365 | ||||
| 2/15 | 水曜 | 11:30~14:30 | 2.0 | 後藤 | 卒業論文 |
| 2/18 | 土曜 | 5:30~11:30 | 6.0 | 後藤 | 卒業論文 |
| 2/20 | 月曜 | 3:30~10:30 | 6.0 | 後藤 | 卒業論文 |
| 2/23 | 木曜 | 3:30~13:00 | 8.0 | 後藤 | 卒業論文 |
| 2/24 | 金曜 | 14:30~17:30 | 3.0 | 後藤 | 卒業論文 |
| 2/27 | 月曜 | 17:30~22:00 | 4.0 | 後藤 | 卒業論文 |
| 2/29 | 水曜 | 13:30~21:30 | 7.0 | 後藤 | 卒業論文 |
| 3/1 | 木曜 | 18:00~21:30 | 3.0 | 後藤 | 卒業論文 |
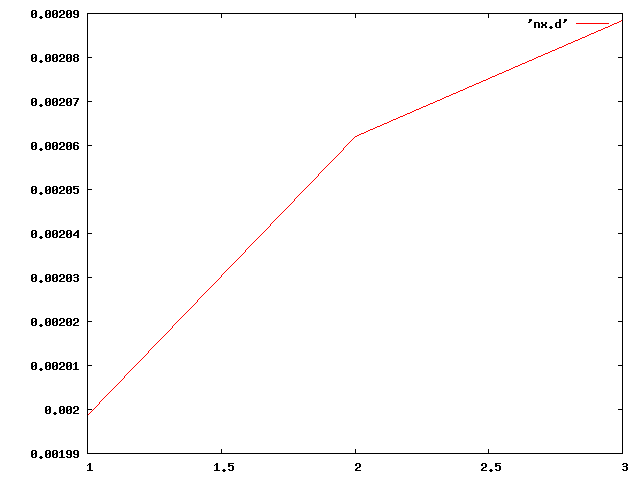
| X軸 |  |
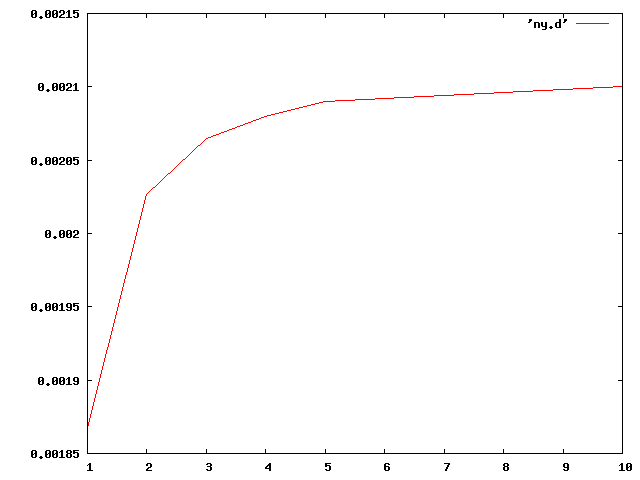
| Y軸 |  |
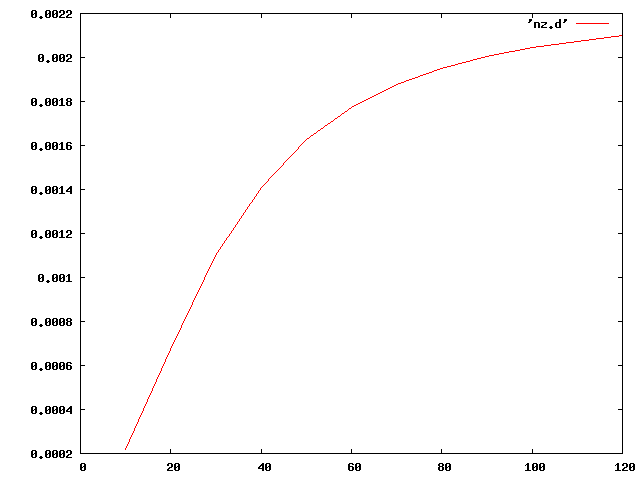
| Z軸 |  |
| ポアソン比=0 | 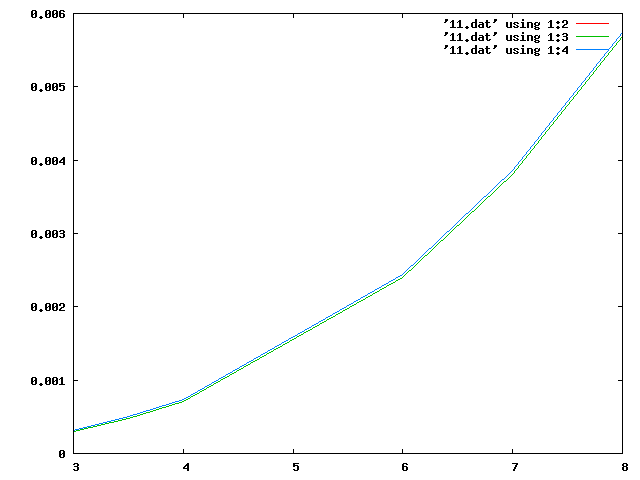 |
| ポアソン比=0.3 | 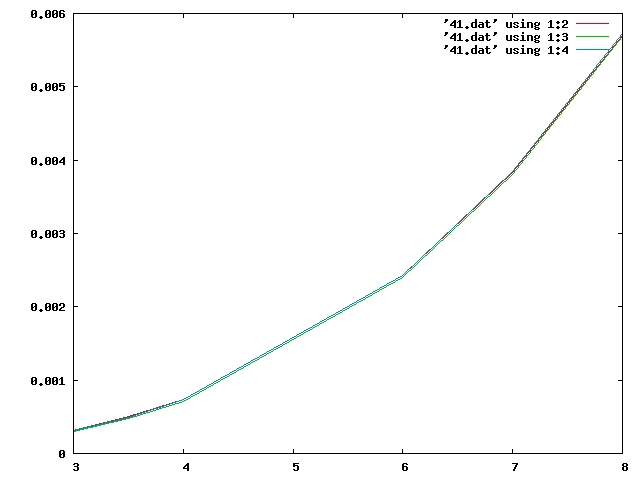 |
| ポアソン比=0.49999 | 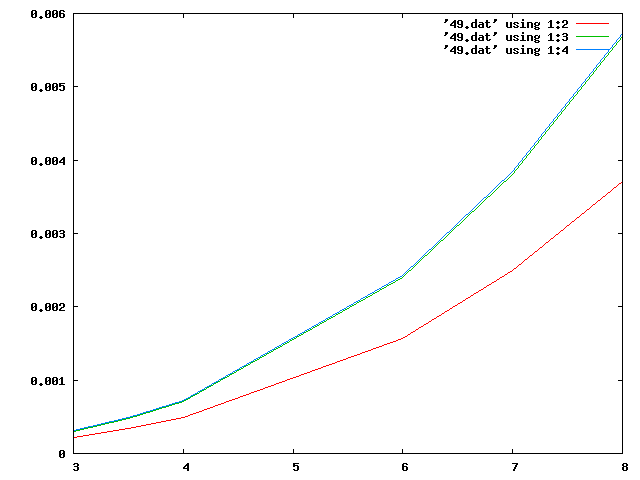 |
横軸に$\frac{\ell}{h}$をとっているので、ケタ高比が大きくなるほどたわみが大きくなる。
グラフは赤が有限要素法での解析結果、緑が初等梁の理論値、青がティモシェンコ梁の理論値を表す。 今回は等方性で解いたため $v=\frac{p{\ell}^{3}}{3EI}+\frac{p\ell}{kGA}$ の $G=\frac{E}{2(1+\nu)}$ が $\frac{E}{3}<G<\frac{E}{2}$の間での変化となるので初等梁とティモシェンコ梁の差がほとんどでなかった。 ちなみにポアソン比を0.5に設定するとcalculixではエラーとなり解析結果がでなかった。
せん断弾性係数$G$とポアソン比$\nu$を設定し、$G=\frac{E}{2(1+\nu)}$よりヤング率$E$を求める。
片持ち梁の解析プログラム kata.f と cghkata.f に$E$を入力し、それぞれのたわみ$v'$、$v''$を求める。
たわみの式(ティモシェンコ)$v=\frac{p{\ell}^{3}}{3EI}+\frac{p{\ell}}{kGA}$より$G'$と$G''$が求められる。
この$G$と$G'$$G''$を比較する。
$G=6.28[GPa]$これは千田さんのプログラムcghkata.fにあった値を使用した。
$\nu=0.016$と$\nu=0.4$は大黒屋さんの卒業論文にあった値を使用した。これはそれぞれ$x$、$y$方向のポアソン比と$z$方向のポアソン比である。
梁の寸法については、実験で使うものの大きさに近い$h=0.15[m]$、$b=0.105[m]$、$\ell=1.3[m]$を設定した。
結果は$E=12.76[GPa]$と$E=17.58[GPa]$が求められた。
この$E$を利用し求められた$v'$は $v'=0.00398[m]$と $v'=0.00275[m]$が求められた。 $v''$は $v''=0.000394[m]$と $v''=0.000307[m]$になった。
この$v'$より、$G'=7.20[GPa]$と $G'=-7.68[GPa]$が求められた。 $v''$より $G''=-0.28[GPa]$と $G''=-0.38[GPa]$になった。
$\nu=0.016$の方はともかく、$\nu=0.4$の方は値が負になってしまった。これは変形した式$G`=\frac{3EIP\ell}{KA(3EIv-P\ell^3)}$において、$\ell$の値が大きいため$(3EIv-P\ell^3)$が負になってしまったためと考えられる。
そもそも$G=\frac{E}{2(1+\nu)}$によって得られる$G$は$0<\nu<0.5$の範囲では$\frac{E}{3}<G<\frac{E}{2}$となるので$G=\frac{E}{15}$に近いとされる木のせん断弾性係数には利用できないものと思われる。
論文「曲げ試験による木材梁のせん断弾性係数推定の精度」より、直交異方性では$G=\frac{E}{2(1+\nu)}$の式は使えないとのこと。
$G''$については2つとも負の値になってしまい、絶対値もかなり小さくなってしまった。これはたわみが1桁小さく出てきたことが原因と考えられる。
①より$G=\frac{E}{2(1+\nu)}$は直交異方性では使えないので、$G=\frac{E}{15}$を使用する。
$G'$は曲げヤング率の逆数$\frac{1}{E'}$と桁高比の2乗$(\frac{h}{\ell})^2$の関係をプロットした図の傾きと切片から求める。
このはじめに設定した$G$と図から求めた$G'$を比較する。
そのために必要な$h$と$\ell$は供試体の寸法を変えて数種類を用意する。
この供試体のたわみ$v$をcalculixで求め、このたわみ$v$を使って、曲げヤング率$E'$を求める。
曲げヤング率は$E'=\frac{P\ell^3}{3Iv}$から求める。
たわみ$v$はkata.fを解析することで求める。ただし直交異方性を考慮するためのプログラムを組んでおく。その際に必要な行列の値はcghkata.inpから得る。区別のためこのkata.fを katao.f とする。
ここでcghkata.fでのヤング率、ポアソン比、せん断弾性係数の設定には注意しておくこと。
!######## 材料の設定 ########
!******** 集成材の材料設定(圧縮) ********
write(7,'("*MATERIAL,NAME=GLUP")')
write(7,'("*ELASTIC,TYPE=ORTHOTROPIC")')
!
! ヤング率:exx,eyy,ezz
! print*,'z軸方向のヤング率を入れて下さい'
! read*, ezz
ezz=9.00d3
! print*,'x軸方向のヤング率を入れて下さい'
! read*, exx
exx=ezz/25.d0
! print*,'y軸方向のヤング率を入れて下さい'
! read*, eyy
eyy=ezz/25.d0
!
! ポアソン比:poixy,poixz,poiyz
poixy=0.016d0
poixz=poixy
poiyx=poixy
poiyz=poixy
poizx=0.4d0
poizy=poizx
!
! せん断弾性係数:gxy,gxz,gxy
gxy=6.00d2
gxz=gxy
gyz=gxy
!
ヤング率はezzに、ポアソン比はpoixyにせん断弾性係数はgxyに入力すること。 つまりヤング率はz軸方向のものを入力する。
やり方として、kata.fに直交異方性の定数を出すプログラムを組み込む(orthoと定義している)。 kata.fに使用する定数はcghkata.fをコンパイルし、出力したcghkata.inp内のORTHOTROPICにある。
例
*ELASTIC,TYPE=ORTHOTROPIC
362.5031, 8.1724, 362.5031, 148.2702, 148.2702, 9118.6161,
600.0000, 600.0000,
600.0000,294
直交異方性材料のひずみ-応力関係の式
$\begin{pmatrix} \epsilon_{x} \\ \epsilon_{y} \\ \epsilon_{z} \\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{pmatrix} = \begin{pmatrix} \frac{1}{E} & -\frac{\nu_{xy}}{E_{x}} & -\frac{\nu_{xy}}{E_{x}} & 0 & 0 & 0 \\ -\frac{\nu_{yx}}{E_{y}} & \frac{1}{E_{y}} & -\frac{\nu_{yz}}{E_{y}} & 0 & 0 & 0 \\ -\frac{\nu_{zx}}{E_{z}} & -\frac{\nu_{zy}}{E_{z}} & \frac{1}{E_{z}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{G_{xy}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{G_{xz}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{G_{yz}} \end{pmatrix} \begin{pmatrix} \sigma_{x} \\ \sigma_{y} \\ \sigma_{z} \\ \tau_{xy} \\ \tau_{xz} \\ \tau_{yz} \end{pmatrix}$
をcghkata.f内で$e66(\circ,\circ)$を使って表す。
対応をまとめると
\begin{pmatrix} e66(1,1) & e66(1,2) & e66(1,3) & \ & \ & \ \\ e66(2,1) & e66(2,2) & e66(2,3) & \ & \ & \ \\ e66(3,1) & e66(3,2) & e66(3,3) & \ & \ & \ \\ \ & \ & \ & e66(4,4) & \ & \ \\ \ & \ & \ & \ & e66(5,5) & \ \\ \ & \ & \ & \ & \ & e66(6,6) \end{pmatrix}
のようになる。
cghkata.f内の材料設定の圧縮と引張の両方で
$e66(1,1), e66(1,2), e66(2,2), e66(1,3), e66(2,3), e66(3,3), e66(6,6), e66(5,5), e66(4,4), '294'$
上記のように設定している。(294は温度のこと=21℃)
cghkata.inpの*ELASTIC,TYPE=ORTHOTROPICに表示される数値はこの順番で出てくる。わかりやすくまとめると
\begin{pmatrix} ① & ② & ④ & \ & \ & \ \\ — & ③ & ⑤ & \ & \ & \ \\ — & — & ⑥ & \ & \ & \ \\ \ & \ & \ & ⑨ & \ & \ \\ \ & \ & \ & \ & ⑧ & \ \\ \ & \ & \ & \ & \ & ⑦ \end{pmatrix}
のようになる。
あとはcghkata.inpの*ELASTIC,TYPE=ORTHOTROPICに出てきた数値を、kata.fのヤング率の所に入力する。入力は2段に分けて行う。 また、kata.fのELASTICの所を"*ELASTIC,TYPE=ORTHOTROPIC" に変更する。
例
print'("*MATERIAL,NAME=EL")'
print'("*ELASTIC,TYPE=ORTHOTROPIC")'
! ヤング率(MPa)とポアソン比(てことは異方性のときはどうすんのかな)
print'(" 362.5031, 8.1724, 362.5031, 148.2702,
148.2702, 9118.6161, 600.0000, 600.0000,")'
print'("600.0000,294")'
print'("*SOLID SECTION,ELSET=Eall,MATERIAL=EL")'
この変更したkata.fをkatao.fとする。
注意 g77でのコンパイルではエラーに注意する。
異方性材料の応力−ひずみ関係の式は
$\begin{pmatrix} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{12} \\ \sigma_{23} \\ \sigma_{31} \end{pmatrix} = \begin{pmatrix} E_{1111} & E_{1122} & E_{1133} & E_{1112}& E_{1123} & E_{1131} \\ \ & E_{2222} & E_{2233} & E_{2212} & E_{2223} & E_{2231}\\ \ & \ & E_{3333} & E_{3312} & E_{3323} & E_{3331} \\ \ & \ & \ & E_{1212} & E_{1223}& E_{1231} \\ \ & \ & \ & \ & E_{2323} & E_{2331} \\ \ & \ & \ & \ & \ & E_{3131} \end{pmatrix} \begin{pmatrix} \epsilon_{11} \\ \epsilon_{22} \\ \epsilon_{33} \\ \epsilon_{12} \\ \epsilon_{23} \\ \epsilon_{31} \end{pmatrix}$
となる。calculixのマニュアルでは、数値の入力の順番を
1段目に
$D_{1111} \ D_{1122} \ D_{2222} \ D_{1133} \ D_{2233} \ D_{3333} \ D_{1212}, \ D_{1313}$
2段目に
$D_{2323} \ Temperature.$
としている。
しかし、これでは
\begin{pmatrix} ① & ② & ④ & \ & \ & \ \\ — & ③ & ⑤ & \ & \ & \ \\ — & — & ⑥ & \ & \ & \ \\ \ & \ & \ & ⑦ & \ & \ \\ \ & \ & \ & \ & ⑨ & \ \\ \ & \ & \ & \ & \ & — \end{pmatrix}
⑧$D_{1313}$がない。
どうやらcalculixのマニュアルと応力-ひずみの関係式は一致していない様なので、calculixのマニュアルでの表示を行列で表してみる。
\begin{pmatrix} D_{1111} & D_{1122} & D_{1133} & D_{1112}& D_{1113} & D_{1123} \\ \ & D_{2222} & D_{2233} & D_{2212} & D_{2213} & D_{2223}\\ \ & \ & D_{3333} & D_{3312} & D_{3313} & D_{3323} \\ \ & \ & \ & D_{1212} & D_{1213}& D_{1223} \\ \ & \ & \ & \ & D_{1313} & D_{1323} \\ \ & \ & \ & \ & \ & D_{2323} \end{pmatrix}
これに番号を付けると
\begin{pmatrix} ① & ② & ④ & \ & \ & \ \\ — & ③ & ⑤ & \ & \ & \ \\ — & — & ⑥ & \ & \ & \ \\ \ & \ & \ & ⑦ & \ & \ \\ \ & \ & \ & \ & ⑧ & \ \\ \ & \ & \ & \ & \ & ⑨ \end{pmatrix}
になる。cghkata.inpでの順番とcalculixのマニュアルでの順番が⑦⑧⑨で異なるが、この値はすべて同じなので今回は問題ない。
以上より、cghkata.inpにて出力される値はそのままの順番でkata.fの"*ELASTIC,TYPE=ORTHOTROPIC"に入力する。
追記
こっちを使った方が楽 kataoa.f
確認として同じ供試体のデータを使い、cghkata.fとkatao.fのたわみを比較してみる。この結果が一致すればわざわざkatao.fを使う必要がなくなる。
もし一致しなければこのやり方で課題を進める。
上記で「$G$は曲げヤング率$\frac{1}{E'}$と桁高比の2乗$(\frac{h}{\ell})^2$の関係をプロットした図の傾きと切片から求める。」とあるが、これはグラフの回帰直線を利用する。
このためのプログラムはkaikisen.fを利用する。これをコンパイルした実行ファイルに(xとyのデータである)~.dを作成し入力する。
結果、回帰直線の傾きaと切片bが求められる。
このkaikisen.fについてはエクセルと同じデータを使用し本当にあっていいるかを確認した。
メモ3よりcghkata.f とkatao.fの比較をする。 (ついでにkata.fも)
供試体のデータは
| 高さ$h=0.96[m]$、幅$b=0.96[m]$、長さ$\ell=1.0[m]$、ヤング率$E=9.00[GPa]$、せん断弾性係数$G=\frac{E}{15}=0.6[GPa]$、荷重$N=1000[N]$、要素分割$x=2$、$y=6$、$z=460$ |
とする。
解析の結果はたわみ$v$が接点番号9670で
katao.fが5.4008E-03[m]、cghkata.fの方がv=-1.0549E-02[m]、kata.fの方が5.2598E-03[m]
となった。
katao.fとkata.fは似たような値となったがcghkata.fはよくわからない値となった。
まずは桁高比を決めるために供試体の高さと長さ(スパン)を設定した。
高さは、$5[cm]$、$9.6[cm]$、$10[cm]$、$20[cm]$
長さは、$0.6[m]$から$1.5[m]$に設定した。
これらの組み合わせにより50点をプロットする。
高さと長さは設定した。
その他は上記の供試体のデータを使用する。
これらの数値をkatao.fに入力し、たわみを出す。
直交異方性でのヤング率、ポアソン比の値は
*ELASTIC,TYPE=ORTHOTROPIC
362.5031, 8.1724, 362.5031, 148.2702, 148.2702, 9118.6161,
600.0000, 600.0000,
600.0000,294
から変化しなかったのでcghkata.inpは一回しか使わなかった。 (ヤング率やポアソン比、せん断弾性係数は変更していないため)
求めたたわみより、曲げヤング率を求める。
この曲げヤング率の逆数と桁高比の2乗の値をkaikisen.fに入力し、傾きと切片を求める。 (1行目はデータの数、2行目から数値を入れる。)
解析結果
| 傾き | 0.471914251 |
| 切片 | 0.110900102 |
グラフにすると
となる。(縦軸にヤング率の逆数$\frac{1}{E'}$、横軸に桁高比の2乗$(\frac{h}{\ell})^2$)
曲げヤング率は$E'=\frac{P\ell^3}{3Iv}$なので、
$\frac{1}{E'}=\frac{3I}{P\ell^3}\times v$
$\frac{1}{E'}=\frac{3I}{P\ell^3}(\frac{P\ell^3}{3EI}+\frac{P\ell}{kG'A})$
$\frac{1}{E'}=\frac{1}{E}+\frac{3\frac{bh^3}{12}P\ell}{P\ell^3kG'bh}$
$\frac{1}{E'}=\frac{1}{E}+\frac{1}{4kG'}(\frac{h}{\ell})^2$
この傾きと切片はそれぞれ$\frac{1}{4kG'}$と$\frac{1}{E}$になるので式を直して、$G$と$E$を求める。※$k=\frac{5}{6}$
解析結果
| $G'$ | 0.63570871 |
| $E$ | 9.017124258 |
相対誤差=(測定値ー理論値)÷理論値 より
| $G'$ | $(0.63570871-0.6)\div 0.6=0.05951452$ | 6.0% |
| $E$ | $(9.017124258-9)\div 9=1.90260538\times 10^-3$ | 0.2% |
また、初等梁とティモシェンコ梁で同じ事をして確認してみる。
解析結果
| 傾き | - |
| 切片 | 0.111111111 |
解析結果
| $G'$ | - |
| $E$ | 9.0000000001 |
相対誤差=(測定値ー理論値)÷理論値 より
| $G'$ | - | - |
| $E$ | $(9.0000000001-9)\div 9=0.00000000001\times 10^-3$ | ≒0 |
初等梁ではG'は使用されない、グラフの式は$y=0.11111111$となるので傾きは求められない。
解析結果
| 傾き | 0.499999096 |
| 切片 | 0.111111134 |
解析結果
| $G'$ | 0.600001084 |
| $E$ | 8.999998146 |
相対誤差=(測定値ー理論値)÷理論値 より
| $G'$ | $(0.600001084-0.6)\div 0.6=1.806667\times 10^6$ | ≒0% |
| $E$ | $(8.999998146-9)\div 9=-2.06\times 10^-7$ | ≒0% |
ティモシェンコ梁での結果はkatao.fと相対誤差がほとんど同じになった。
さらに比較としてkata.fでのたわみでも相対誤差を出してみる。
解析結果
| 傾き | 0.0666849426 |
| 切片 | 0.111042622 |
グラフにすると
解析結果
| $G'$ | 4.498766713 |
| $E$ | 9.00555104 |
相対誤差=(測定値ー理論値)÷理論値 より
| $G'$ | - | - |
| $E$ | $(9.00555104-9)\div 9=6.167821858\times 10^-4$ | 0.06% |
桁高比を変える時、供試体の大きさも変更していたのでそれにあわせて要素分割数も変更し直すべきだったかもしれない。
実験は供試体の3点曲げ試験を行う。この実験によりたわみがわかりそこからヤング率、せん断弾性係数がわかる。
内容は両端支持の梁の真ん中を中心に任意の面積の分布荷重をかけ、たわみを求める。 支持の面積と荷重をかける面積は設定できる。(計算上では集中荷重)
両端支持の始点側の1列目は固定支承、始点側の残りの部分と終点側の支承はローラー支承となっている。
支承の面積を大きくするには、hari.fのnnの値を大きくすればいい。
荷重をかける面積は梁の中心を軸にして設定する。
面積を大きくするには、mmの値を大きくすればいい。
分布荷重に関係してZ軸方向の要素数は偶数にした方がいい。
上記のhari.fは cghkata.f
を使って直交異方性のヤング率を求めて入力しなければならない。
しかしharioa.fのなかにはcghkata.fですべきことは入っているのでそのまま使える。
注意としてnn=0とする(両端の一番端のみの)場合は、BOUNDRYのSHITANとSHUTANを消すこと。消さないとcalculixで解析できない。
上記のharioa.fでは供試体の1番端に支承があるため正確な解析結果が出ない。 このharioas.fでは両端のあまりの部分、もしくはスパンを設定できるようにしてある。
ちなみにこのharioas.fであまりの部分を0にすると、harioa.fとたわみが同じになる。
こちらの場合でも支承の面積を1とする場合にはROLLIが拘束されないため、inpでROLLIを消さなければならない。
上記と同様に直交異方性を考慮した、片持ち梁のプログラム。 katao.fと同じ結果が出たのでこちらを使った方が楽で確実。
harioa.fの解析結果と理論値でどのくらいの誤差があるのか確認する。
供試体のデータは
| 高さ$h=0.96[m]$、幅$b=0.96[m]$、長さ$\ell=1.0[m]$、ヤング率$E=9.00[GPa]$、せん断弾性係数$G=\frac{E}{15}=0.6[GPa]$、荷重$N=1000[N]$、要素分割$z=400$ |
とする。
比較の対象は初等梁とティモシェンコ梁の計算結果を利用する。 要素分割数については、Z軸の分割数のみ決定し、X軸とY軸の分割数は変化させて対象に最も近くなったものを利用する。
というのも、この大きさの供試体では要素数分割$x=2$、$y=6$、$z=460$が最適だったがharioa.fはZ軸の分割数によって支承や荷重のかかる面積が決定するのでキリのいい数値にしなければ面積がわかりづらくなってしまうので。
↓↓
結局、要素数分割は$x=2$、$y=6$、$z=400$になった。 (Yを8にするとセグメンテーション違反になってしまうため。)
harioa.fの解析結果が理論値と一致するかどうかを確かめる。
harioa.fはnn=0(つまり両端の一番はじっこのみ拘束)とし、荷重もmm=0(真ん中の1列のみ載荷)とする。
理論値は公式の$v=\frac{P\ell^3}{48EI}$(初等梁)と$v=\frac{P\ell^3}{48EI}+\frac{P\ell}{4kGA}$(ティモシェンコ梁)を利用する。
結果は
| harioa.f | 4.1151E-04 |
| 初等梁 | 0.0003270488 |
| ティモシェンコ梁 | 0.0003813023 |
となった。
結果が一致しなかった理由としてcgxで確認したところ、載荷している1列のみ力がかかっているのでそこだけ異常に引っ張られたり切れ込みのようになっていたことが挙げられると思う。
改善点として、載荷の面積をもう少し増やしてみる(mmを大きくする)ことで理論値に近づくかもしれない。また、支承の面積を増やして(nnを大きくして)確認する必要もある。
mmとnnの増減
| nn\mm | 0 | 1 | 2 | 3 | 4 | 5 | 30 | 60 |
| 0 | 4.1151E-04 | 4.1149E-04 | 4.1146E-04 | 4.1140E-04 | 4.1133E-04 | 4.1125E-04 | 4.0514E-04 | 3.9090E-04 |
| 1 | 3.9799E-04 | 3.9796E-04 | 3.9793E-04 | 3.9787E-04 | 3.9781E-04 | 3.9773E-04 | 3.9165E-04 | 3.7749E-04 |
| 2 | 3.8788E-04 | 3.8785E-04 | 3.8782E-04 | 3.8777E-04 | 3.8770E-04 | 3.8762E-04 | 3.8157E-04 | 3.6749E-04 |
| 3 | 3.8110E-04 | 3.8107E-04 | 3.8104E-04 | 3.8098E-04 | 3.8092E-04 | 3.8084E-04 | 3.7480E-04 | 3.6079E-04 |
| 4 | 3.7209E-04 | 3.7206E-04 | 3.7203E-04 | 3.7197E-04 | 3.7191E-04 | 3.7183E-04 | 3.6583E-04 | 3.5190E-04 |
| 5 | 3.6522E-04 | 3.6520E-04 | 3.6517E-04 | 3.6511E-04 | 3.6505E-04 | 3.6497E-04 | 3.5899E-04 | 3.4514E-04 |
以上より等方性ではmmを増やしても大きな変化がないので、上辺の引張や切れ込みによる中心部のたわみへの影響は少ないと考えられる。
それよりもnnを増やしたことによるスパンの変化の影響が大きかった。(もしくは支承の要素数の増大による影響)
なので今度計算する場合は供試体の長さだけでなくスパンも考慮した方がいいかもしれない。
この供試体に対する最適な分割数をもう一度探してみる。
条件として長さ=スパンである(はじっこの部分がない)こと、ヤング率が210GPaの等方性であることとする。またx軸の分割数は2で固定とする。
ティモシェンコ梁のたわみは$v=0.00014419$だった。
ny=6
| nz | 360 | 380 | 400 | 420 | 440 | 460 | 478 |
| たわみ | 0.000014298 | 0.000014298 | 0.000014299 | 0.0000143 | 0.0000143 | 0.000014301 | 0.000014301 |
| 分割数 | 7581 | 8001 | 8421 | 8841 | 9261 | 9681 | 10059 |
ny=8
| nz | 260 | 280 | 300 | 320 | 340 | 360 | 370 |
| たわみ | 0.000014328 | 0.00001433 | 0.000014332 | 0.000014334 | 0.000014335 | 0.000014335 | 0.000014335 |
| 分割数 | 7047 | 7587 | 8127 | 8667 | 9207 | 9747 | 10017 |
ny=10
| nz | 200 | 220 | 240 | 260 | 280 | 300 | 302 |
| たわみ | 0.000014337 | 0.00001434 | 0.000014345 | 0.000014347 | 0.000014348 | 0.000014351 | 0.000014352 |
| 分割数 | 6633 | 7293 | 7953 | 8613 | 9273 | 9933 | 9999 |
ny=12
| nz | 160 | 180 | 200 | 220 | 240 | 256 |
| たわみ | 0.000014336 | 0.000014341 | 0.00001435 | 0.000014352 | 0.000014358 | 0.00001436 |
| 分割数 | 6279 | 7059 | 7839 | 8619 | 9399 | 10023 |
ny=14
| nz | 140 | 160 | 180 | 200 | 220 | 222 |
| たわみ | 0.000014331 | 0.000014343 | 0.000014348 | 0.000014357 | 0.000014359 | 0.000014359 |
| 分割数 | 6345 | 7245 | 8145 | 9045 | 9945 | 10035 |
ny=16
| nz | 120 | 140 | 160 | 180 | 196 |
| たわみ | 0.000014319 | 0.000014336 | 0.000014348 | 0.000014353 | 0.000014362 |
| 分割数 | 6171 | 7191 | 8211 | 9231 | 10047 |
ny=18
| nz | 120 | 140 | 160 | 174 |
| たわみ | 0.000014322 | 0.000014339 | 0.000014351 | 0.000014356 |
| 分割数 | 6879 | 8079 | 9177 | 9975 |
以上より最もたわみが大きかったのはny=16、nz=196の時だった。
この結果からわかることとして、たわみが大きくなるのは要素分割数が多い時であり、その中でもy方向の分割数が多い場合のたわみが最も大きくなることがわかった。
今回使うharioas.fではスパンの長さを決めるのにz軸の要素を基準とするため計算しやすい要素数に設定する必要がある。そのためnz=200とし、ny=14とする。
ちなみにnz=100、ny=32ではたわみは0.000014302だった。
さらにnx=4で試してみたところnx=2の時よりも値が近づいたので収束値を探してみる。
| ny | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| nz | 222 | 180 | 152 | 132 | 116 | 104 | 94 |
| たわみ | 0.000014408 | 0.000014415 | 0.000014415 | 0.000014407 | 0.000014397 | 0.000014384 | 0.000014369 |
| 分割数 | 10035 | 9955 | 9945 | 9975 | 9945 | 9975 | 9975 |
結果としてnx=2の時よりも、nx=4の時のほうがティモシェンコ梁の値に近づいた。 最も近づいたのがny=10,12の時だがそこからは値が小さくなっていった。 収束の条件として、nyが大きくてなおかつ要素分割数が大きいということがあるがそれに加えてある程度のnxと、nzの分割数にも限界があることがわかった。
以上より、最適な要素分割数を求めたが実際に解析に利用する分割数としてはnz=200とするのが最もよさそうなのでnx=4,ny=8,nz=200というように分割する。
この場合のたわみは1.4406E-05となった。
harioa.fではこの部分がないので結果が合わなかった可能性がある。
そこで今度ははみ出た部分を設定できる harioas.f で解析して結果を見てみる。
まずは等方性のまま試してみる。支承の要素数は1列とする。
ティモシェンコ梁で供試体の長さを変えて計算してみる。
同時にharioas.fでも梁の長さはそのままでスパンを変更して解析してみる。
| 計算法\スパンの長さ | 0.7 | 0.8 | 0.9 | 1.0 |
| ティモシェンコ | 5.0897E-06 | 7.4988E-06 | 1.0581E-05 | 1.4419E-05 |
| harioas.f | 5.0576E-06 | 7.4492E-06 | 1.0510E-05 | 1.4406E-05 |
結果は多少の誤差はあるがほぼ同じ値となった。 等方性ではこのやり方で解析できることがわかった。
今までは載荷部と支承部を直接拘束していたが、載荷部と支承部のそれぞれに鋼板を敷きその上から荷重を載荷、もしくは鋼板の真ん中1列を拘束するようにした。これで実際の3点曲げの状態に近くなったと思われる。
kai2.f は支承部は下に鋼板を敷いたが載荷部はそのままつまり分布荷重にしてある。
kai3.f は載荷部も鋼板になっていて、その鋼板の真ん中1列に載荷するようになっている。
このkai2.fとkai3.fを比べた結果こちらのほうが少しだけティモシェンコの式に近づいた。 また鋼板のヤング率も206[GPa]と1000[GPa]で試したところ1000[GPa]の方が近くなった。
kai3.f と harioas.f と、ティモシェンコの式の結果を比較しグラフを作成する。
供試体は今までのものと同じものを利用する。 (幅は10cm) 高さと長さ(スパン)は
| 高さ10cm | |
| 長さ(スパン) | 0.5m~1.0m |
と設定した。 (プロットするのはこれらの組み合わせ10点。) (長さは供試体の長さではなく、スパン)
この3つの解析計算結果を
縦軸(たわみ)-横軸($\frac{\ell}{h}$)
と
縦軸($\frac{1}{E'}$)-横軸($(\frac{h}{\ell})^2$)
の2つのグラフに表す。
要素数はnx=4,ny=8,nz=200で支点部と載荷部の要素数は2要素とした。
また今回は高さを変えずに桁高比を変えるためスパンだけを変更する。 利用するスパンは
0.98m、0.95m、0.90m、0.85m、0.80m、0.75m、0.70m、0.65m、0.60m、0.55m、0.50m
の11点とする。最大値が0.98mの理由は支点から端部までの間に自由な1要素と鋼板の要素の半分である1要素が必要となったから。
このスパンでのティモシェンコのたわみは vtim.d となった。
またkai3.fのたわみは vkai.d となり、
harioas.fのたわみは vhari.d となった。
桁高比$\frac{\ell}{h}$は keta.d となりこれらの結果をまとめたグラフが
(赤がティモシェンコ、青がharioas.f(鋼板なし)、緑がkai3.f(鋼板あり))
このような結果になった。 この場合のティモシェンコに対するkai3.f(鋼板あり)とharioas.f(鋼板なし)の相対誤差のグラフが
(赤がkai3.f(鋼板あり)、緑がharioas.f(鋼板なし))
である。
グラフからkai3.f(鋼板あり)の方が、誤差が小さくなっていることがわかる。
このグラフの右側で極点ができている理由として、支点部の鋼板と端部の距離が短すぎて、正確な解析が出来なかったと考えられる。
また左側に行くに連れて誤差が大きくなる。この部分は有限要素法での誤差だと思われるので、左側のいくつかの点と右側の誤差の部分ははじいてグラフにするとこのようになる。
この2つの線の差が鋼板有りのモデルと無しのモデルの差だと言える。
ここでプロットした点が11点のものと5点のものの両方で回帰直線のグラフを作り、せん断弾性係数を求める。
縦軸の求め方は片持ち梁の場合と同じで$v=\frac{P\ell^3}{48EI}$(初等梁)と$v=\frac{P\ell^3}{48EI}+\frac{P\ell}{4kGA}$(ティモシェンコ梁)を利用する。
$\frac{1}{E'}=\frac{48I}{P\ell^3}\times v$
$\frac{1}{E'}=\frac{48I}{P\ell^3}(\frac{P\ell^3}{48EI}+\frac{P\ell}{4kG'A})$
$\frac{1}{E'}=\frac{1}{E}+\frac{48\frac{bh^3}{12}P\ell}{P\ell^3 4kG'bh}$
$\frac{1}{E'}=\frac{1}{E}+\frac{1}{kG'}(\frac{h}{\ell})^2$
(青い線がティモシェンコ、赤い線がkai3.f(鋼板あり)、緑の線がharioas.f(鋼板なし))
11点のもの
| 傾き | 切片 | せん断弾性係数[GPa] | ヤング率[GPa] | |
| ティモシェンコ | a= 1.999 | b=0.111 | 0.600 | 9.000 |
| kai3.f(鋼板あり) | a=2.434 | b=0.108 | 0.493 | 0.259 |
| harioas.f(鋼板なし) | a=2.808 | b=0.106 | 0.427 | 9.434 |
(青い線がティモシェンコ、赤い線がkai3.f(鋼板あり)、緑の線がharioas.f(鋼板なし))
5点のもの
| 傾き | 切片 | せん断弾性係数[GPa] | ヤング率[GPa] | |
| ティモシェンコ | a=2.00 | b=0.111 | 0.600 | 9.000 |
| kai3.f(鋼板あり) | a=2.238 | b=0.110 | 0.536 | 9.091 |
| harioas.f(鋼板なし) | a=2.552 | b=0.109 | 0.476 | 9.174 |
| 厚さ | 長さ(載荷部) | 長さ(支点部) | |
| 変更前 | 1mm | 1cm | 1cm$\times$2 |
| 変更後 | 5mm | 10cm | 5cm$\times$2 |
鋼板を上記のように変更した。これでより実際の試験の状態に近づいた。
鋼板あり(変更後)
たわみ−桁高比
今回はスパンを0.5mから0.9mの間の9点でプロットした。 (5点のものは0.7mから0.9m)
ティモシェンコ梁と鋼板あり、鋼板なしとの誤差
ティモシェンコ梁を基準としているので、ティモシェンコ梁の誤差は0%となっている。
$\frac{1}{E_{曲げ}}$-$(\frac{h}{\ell})^2$のグラフ
9点の場合
| 傾き | 切片 | せん断弾性係数[GPa] | ヤング率[GPa] |
| a=1.571 | b=0.103 | 0.764 | 9.709 |
5点の場合
| 傾き | 切片 | せん断弾性係数[GPa] | ヤング率[GPa] |
| a=1.456 | b=0.105 | 0.824 | 9.524 |
単純支持梁のたわみを求めるプログラム(直交異方性)
載荷と拘束は直接解析モデルの要素を選んで行っている。載荷幅と拘束幅は調節できる。 ただし要素単位で指定するのでz軸の要素数をうまく設定しないと望んだ幅の長さにならない。例として軸方向要素数nzを200に、長さを1mとすると、1要素あたり0.5cmとなり設定しやすい。
スパンを調節するには、端部から支点の始まる部分の要素数を決め手調節する。
支点部のうち片方の1列目は固定されている。(KOTEI)
2列目からと、もう片方の支点部は水平に移動する。(ROLLI)(ROLLU)
支点部を1列しか設定しない場合はROLLIをinpファイルにしないよう消さなければならない。
単純支持梁のたわみを求めるプログラム(直交異方性)
こちらは解析モデルの上と下に鋼板を置きその鋼板の要素に載荷、拘束しを行えるようにした。
鋼板の幅は自由に決められるが、載荷拘束をするのは鋼板の真ん中1列だけ。また、こちらも設定はz軸の要素数に依存するのでうまく調節する必要がある。
拘束については片方は固定、もう片方は水平に移動する。
| 接着剤名 | ディアノール |
| 硬化剤名 | (くるみの殻) |
接着剤$X$[g]に対して損失率1.3を考慮する。つまり必要な接着剤は$X+0.3X$[g]となる。
硬化剤の量は接着剤の15%とする。つまり必要な硬化剤は$(X+0.3X)\times0.15$[g]となる。
| No | E(GPa) |
| 116 | 4.135 |
| 72 | 4.146 |
| 47 | 4.156 |
| 20 | 5.949 |
| 110 | 6.043 |
| 3 | 6.047 |
| 69 | 7.120 |
| 55 | 7.130 |
| 15 | 7.135 |
| 148 | 7.976 |
| 66 | 7.994 |
| 143 | 8.040 |
| No | E(GPa) |
| 89 | 3.876 |
| 32 | 3.885 |
| 5 | 3.937 |
| 18 | 6.167 |
| 49 | 6.174 |
| 29 | 6.180 |
| 142 | 6.895 |
| 23 | 6.900 |
| 109 | 6.933 |
| 105 | 8.658 |
| 123 | 8.687 |
| 22 | 8.694 |
供試体を作成する。
供試体の曲げ試験を行いたわみ$v$を求める。
$v$を$v=\frac{P\ell^3}{3E'I}$に代入し、曲げヤング率$E'$を求める。
ここで$\frac{1}{E'}$と$(\frac{h}{\ell})$の関係をプロットすると、回帰直線の切片と傾きからヤング率$E$と、せん断弾性係数$G$が求められる。
関係をプロットするため、何度かスパンを変えて試験を行う。この時スパンは桁高比に合わせて設定する。
時間の関係で実験は中止となった。
研究は解析のみを行い結果をだす。
参考 http://www.waka.kindai.ac.jp/tea/shibue/abaqus-inpexp.html
参考 http://freecaetester.blog62.fc2.com/blog-entry-15.html
参考 http://freecaetester.blog62.fc2.com/blog-entry-183.html
マニュアルP167
直交異方性で解析を行う場合はELASTICのところをTYPE=ISOではなく、ORTHOTROPICにする。
"*ELASTIC,TYPE=ORTHOTROPIC"
その後に直交異方性でのヤング率とポアソン比を入力すればいい。 ただし、1段目と2段目に分けて入れる必要がある。
cgxを使っているときに
plot ea all
と入力すると要素と要素番号を教えてくれる。
また、
plot na all
と入力すると節点番号を教えてくれる。
同時に見たい場合は
plot na all plus ea all
と入力すればいい。
まずはサイトからlibreofficeをダウンロードし、 適当なところへ保存する。(rpm/RPMS/i386) その後は
---ダウンロードしたファイルを解凍 $ tar zxf LibO_3.4.2_Linux_x86_install-rpm_en-US.tar.gz ---解凍してできるLibO_3.4.2rc3_Linux_x86_install-rpm_en-USの中のRPMSに移動 $ cd LibO_3.4.2rc3_Linux_x86_install-rpm_en-US/RPMS/ ---RPMSディレクトリの中にあるインストーラーをすべて実行 $ sudo rpm -Uvh *.rpm ---RPMSの中にあるdesktop-integrationディレクトリに移動 $ cd desktop-integration/ ---ショートカット作成用のインストーラーを実行 $ sudo rpm -Uvh *redhat*.rpm
なぜか競合してうまくいかなかったので、 libreoffice3.5-freedesktop-menus-3.5-13.noarch.rpm だけrpmで実行したらとりあえず起動できた。
次に日本語化をする
---ダウンロードしたファイルを解凍 $ tar zxf LibO_3.4.2_Linux_x86_langpack-rpm_ja.tar.gz ---解凍してできるLibO_3.4.2rc3_Linux_x86_langpack-rpm_jaの中のRPMSに移動 $ cd LibO_3.4.2rc3_Linux_x86_langpack-rpm_ja/RPMS/ ---RPMSディレクトリの中にあるインストーラーをすべて実行 $ sudo rpm -Uvh *.rpm
ファイルの属性を変更する。
$chmod 744 test
数字は属性を表す。
| r | 読み込み |
| x | 実行 |
| w | 書き込み |
| 4 | r-- |
| 5 | r-x |
| 6 | rw- |
| 7 | rwx |
数字の位置は操作可能な人を表す。
| 7 | 4 | 4 |
| 自分 | グループ | 他人 |
オプション
| -i | 大文字、小文字を無視する。 |
| -b | 空白の数を無視する。 |
| -a | テキストとして処理する。 |
| -q | ファイルが異なるかどうかだけ報告する。 |
a.f
test
tamesi
reidai
renshu
b.f
test
tamesi
rei
renshu
$diff a.f b.f 3c3 < reidai --- > rei
画像ファイルの確認 png等
$eog a.png
こちらは.epsや.pdfを見るときに使う。
例
a.d
1 2 3
b.d
4 5 6
$paste a.d b.d > c.d
c.d
1 4 2 5 3 6
現在のディレクトリを表示する。
$pwd /home/kiso/
予め行う作業を決めておき、オートで実行する。
$vi test ccx_1.7 tamesi1 > tamesi1.kekka ccx_1.7 tamesi2 ccx_1.7 tamesi3 $chmod 744 test $./test
ps ux で確認。
tamesi1.kekkaはtamesi1の解析中のログを保存している。
print'("*ELASTIC,TYPE=ORTHOTROPIC")'
print'(" 362.5031, 8.1724, 362.5031, 148.2702,
148.2702, 9118.6161, 600.0000, 600.0000,")'
print'("600.0000,294")'
をg77でコンパイルしてinpにすると
*ELASTIC,TYPE=ORTHOTROPIC 362.5031, 8.1724, 362.5031, 148.2702, 48.2702, 9118.6161, 600.0000, 600.0000, 600.0000,294
となり、148.2702が48.2702になってしまう。
文末と文頭に&をつける。
print'("*ELASTIC,TYPE=ORTHOTROPIC")'
print'(" 362.5031, 8.1724, 362.5031, 148.2702,&
&148.2702, 9118.6161, 600.0000, 600.0000,")'
print'("600.0000,294")'
このとき他の場所で2行になっているところも同じようにする。(文末と文頭に&を付ける。)
コンパイルはg77ではなくg77fでやればうまくいく。
参考 http://www.str.ce.akita-u.ac.jp/~gotou/tebiki/tex.html
参考 http://web.archive.org/web/20041012065336/http://cse.naro.affrc.go.jp/takezawa/tex/index.html
>pl 'a.d' ,\ 'b.d'
test.dのグラフをpngにして保存する。
>set term png >set output'test.png' >pl 'test.d'
test.dのグラフをepsにして保存する。
set term post eps enhanced color set output'test.eps'
さらに目盛りとラベルの文字の大きさを決める。
set term post eps enhanced color "Arial" 25 set output'test.eps'
set xl '{/=30 test.d}'
set yl '{/=30 test.d}'
>set size square >set xrange [-4:6] >set yrange [2:10]
unset key
例 $y=2x^2+4x+2$をグラフに表す。
>a=2 >b=4 >c=2 >f(x)=a*x**2+b*x+c >pl f(x)
例 $y=3x+2$と$y=5x+4$を同じグラフに表す。
>a=3 >b=2 >c=5 >d=4 >plot a*x+b,c*x+d
もしくは
>a=3 >b=2 >c=5 >d=4 >plot a*x+b, >replot c*x+d
こちらは追加という形になる。
参考 http://t16web.lanl.gov/Kawano/gnuplot/
解像度を変更しシャットダウン。その後起動したらディスプレイが荒れた状態でフリーズしてしまった。
解決策
起動画面のGNU GRUBの場面で起動するカーネルのところでeを押す。次の画面でカーネルを選択(2行目)しeを押す。 コマンド画面になるので表示されている文に続いて singleと入力する。 最後にbを押して起動する。
シングルモードで起動するとsuでコマンドが打てるようになる。
/etc/X11/xorg.conf
を削除し、suを終了すると普通に起動できる。
kata.f(元の名前はccxkata.f)