cgxで要素番号と節点番号を出力して載荷点の番号を確認。
表示する方法は以下の通り
cgx_1.7 ***.frd または cgx_1.7 -c ***.inp
(※cgxのウィンドウが手前に表示された状態で)
plot ea all
plus na all
[単位]
荷重は[MN]・時間は[sec]・長さは[m]・ヤング率は[MPa]=[MN/m^2]としているので、
密度は2800[kg/m^3]であったら2.8d-3と設定する。
質量の単位が不明確だったが、固有値解析で各振動数を理論値と比較したところ
誤差が微小だったので以下の解釈で正しいと思う。
1[N]=1[kg]×9.8[m/sec^2]
荷重と時間と長さを元のプログラム通り揃えると…
1[MN]=1000[t]×9.8[m/sec^2]
なので、質量の単位はプログラムにおいて1なら1000[t]と認識される。
よって密度は2800[kg/m^3]であったら2.8d-3と設定する。
[材料定義]
■*DENSITY…固有値解析する場合に必要となる。(以下はアルミの材料諸元)
→ヤング率,ポアソン比などのあとに密度を定義。
アルミの比重を2800[kg/m^3]として設定している。
たわみを解析する際に密度を設定しても自重によるたわみは考慮されない。
print'("*MATERIAL,NAME=EL")'
print'("*ELASTIC")'
print'("70.d3, 0.33")'
print'("*DENSITY")'
print'("2.8d-3")'
[荷重関連]
■*DLOAD…要素面に対して等分布荷重(圧力)をかけたい時に使用する。
print'("*STEP")'
print'("*STATIC,SOLVER=SPOOLES")'
print'("*DLOAD")'
print'("Eall,P1,1")'
↑載荷したい要素のセット名または番号(Eall)を指定した後、面番号(P1)を指定。
単位面積当りの荷重の大きさを1[MPa]として設定している。
モデルの自重によるたわみを解析したい場合の使用方法
(※*ELASTICで*DENSITYの設定が必要となる ← 定義していないとエラー)
print'("Eall,GRAV,9.8,0.,0.,1.")'
これでEallに対して9.8[m/sec^2]の重力加速度で+Z方向の自重による変位が分かる。
シェル要素であっても解析可能である。
★シェル要素の場合は要素面の垂線方向にしか載荷できないため、
Pのあとに面番号を入力しても値に変化はない。(Pのみでも解析可)
■*AMPLITUDE…時間ごとに載荷する荷重を設定したい場合に使用する。
print'("*AMPLITUDE,DEFINITION=TABULAR,NAME=A1")'
print'("0.,0.,1.d-1,1.,2.d-1,0.,3.d-1,0")'
↑0秒で0,0.1秒で1,0.2秒で0,0.3秒で0,という風に、
時間.,荷重.,時間.,荷重.,…と設定していく。
定義した時間-荷重セットはA1などとして名前をつける
print'("*AMPLITUDE,DEFINITION=TABULAR,NAME=A2")'
print'("*INCLUDE,INPUT=no1.csv")'
↑正弦波などを入力したい場合、人力では限界があるので、
表計算ソフトなどを利用して細かい時間-荷重データを作成し、
csvファイルなどにそのデータをコピーして使用する。(例ではno1.csv)
csvファイルへの書き方は
0., 0.,
1., 0.1,
2., 0.2,
3., 0.3,
*., *.,
*., *.,
と縦に並べていく。時間と荷重の後にはカンマが必要。
print'("*CLOAD,AMPLITUDE=A1")'
print'("LAST,2,5.d-6")'
↑設定した時間-荷重セットを*CLOADや*DLOADのあとに指定。
あとは、普通に (節点・載荷方向・大きさ) を設定する。
[固有値解析]
■*FREQUENCY…固有振動数を指定したモード数だけ算出する。
→モード解析など過渡応答解析をする場合に必要となり、
ここで計算したモード数が多いほど精度が上がる模様。
cgxにおいてモード(振動数)を指定してアニメーションを見ることで
各モードの振動形を確認できる。振動数が低い方から順に表示される。
print'("*STEP")'
print'("*FREQUENCY,SOLVER=SPOOLES,STORAGE=YES")'
print'("20")'
詳しい結果については、目次より
「*FREQUENCYで確認できる振動モードについて」を参照
[モーダル法による過渡応答解析]
■*MODAL DYNAMICS…モード解析する場合に使用。
→時間ステップと解析したい時間の長さを指定する。
このオプションの前の*STEPで*FREQUENCYによる解析が必要となる。
レーリー減衰を設定したい場合には、*MODAL DAMPING を用いる。
print'("*STEP")'
print'("*MODAL DYNAMIC")'
print'("2.d-2,100.d-2")'
print'("*MODAL DAMPING")'
print'(",,0.,2.d-5")'
↑0.02秒ごとに1秒までの解析結果が表示される。
減衰の設定についてはページ先頭の目次より
「減衰の設定について(ccxマニュアル)」
[積分法による過渡応答解析]
■*DYNAMIC…直接積分法によって解析する場合に使用。
→*MODAL DYNAMICと同じく、時間ステップと解析したい時間を指定する。
時間ステップ通りに結果を出力する方法とプログラムによって
自動的に不規則な時間ステップで結果を出力する方法がある。
print'("*STEP,INC=100000000")'
print'("*DYNAMIC,EXPLICIT")'
print'("2.d-2,100.d-2")'
↑EXPLICITを使用すると設定した時間通りに結果を表示できるはずだが、
今のところ解析中にエラーが表示され成功していない。
■*STEADY STATE DYNAMICS…周波数応答解析をするオプション。
どの周波数の荷重に対して応答スペクトルが大きくなるかをグラフ化できるが、
calculixの場合、1ステップごとに実部aと虚部bで2つ出る答えをエクセル
で\sqrt[(a^2+b^2)]で計算すればグラフ化できる。
おそらく変位応答スペクトルで評価しており、
加速度応答や速度応答ではない可能性が高い。
スペクトルが最大になるのは基本的に固有振動数なので、
固有振動数が解析できる場合に利用するかは微妙なところ…
ちなみに[*MODAL DAMPING]で減衰を設定していないと、
固有振動数付近で -NAN となり、その周波数での結果が
確認できなくなるようだ。減衰を設定していると、最大応答スペクトルが小さくなる。
減衰を効かせたくない場合は、減衰の設定を極小にする必要があると思われる。
print'("*STEP")'
print'("*STEADY STATE DYNAMICS")'
print'("1000.,2000.,1.,3")'
周波数範囲の下限と上限を指定
分割パラメータ数の指定(5~10くらいで十分だと思う)
バイアスの指定←デフォルト1
バイアスの設定を変えると、スペクトルが卓越する周波数付近で
点を細かくとるため、応答の極大値をより正確に知ることができる。
※周波数応答は固有値解析とモード解析の結果が一致していれば、 十分な精度が期待できると考えられるので省略する。 また、シェル要素のモード解析では、載荷点のヤング率を極端に大きくしないと、 自由端で変位がバラバラになるため、B32要素で自由端節点の剛性を上げる。
厚さを変えて、固有値解析を行った結果を以下に示す。 断面は幅20mm・軸長200mm・厚さを2mm〜20mmで正方形断面まで変化した。
| 2mm | 理論値 | 解析結果 | 相対誤差 | 5mm | 理論値 | 解析結果 | 相対誤差 | |
| solid | 40.3805 | 43.3120 | 7.258% | 100.9513 | 102.8574 | 1.888% | ||
| shell | 40.3805 | 42.20122 | 4.509% | 100.9513 | 102.0638 | 1.102% | ||
| 10mm | 理論値 | 解析結果 | 相対誤差 | 20mm | 理論値 | 解析結果 | 相対誤差 | |
| solid | 201.9027 | 209.6948 | 3.859% | 403.8053 | 403.6219 | 0.04543% | ||
| shell | 201.9027 | 194.6249 | 3.605% | 403.8053 | 344.1009 | 14.79% |
正方形断面はさすがに解析精度が落ちたが、 薄い断面に関しては、シェル要素の方が分割数が少ないのに精度は高かった。 シェル要素は10×10だったが、ソリッド要素は厚みがなくなると、 厚さ方向の分割数に限界が来るため、代わりに軸方向の分割数を極端に増やして、 解析精度を高めた。(x20y0z200など)それでもなお、シェル要素が優っていた。 以上より、固有値解析の精度を確認。
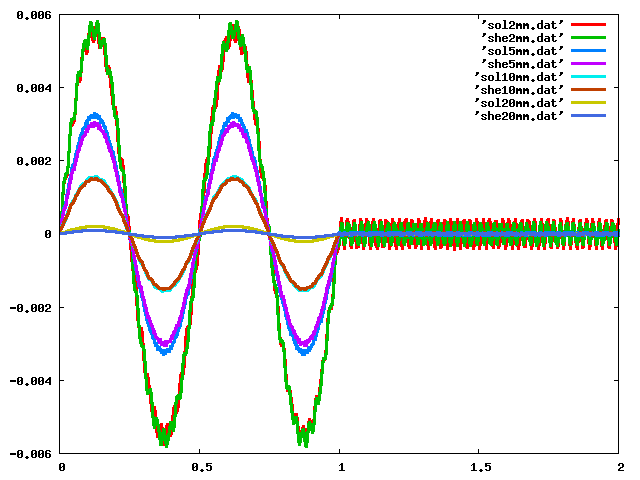
モード解析の結果を以下のグラフに示す。
 |
(http://www.alde.co.jp/advc/examples/shell-solid/index.html)
 |
 |
$損失係数 \eta = 2 \zeta = \frac{|f2-f1|}{fmax}$ 解析パラメータ数を増やして、より滑らかなグラフになるようにして、 最大スペクトルの半分ができるだけ分かるようにする。 だいたいζ=0.05という結果に落ち着き、0.03より大きい結果となった。
| 周方向分割 | 初期高さ | 減衰定数 | |
| 軸方向 | 4 | 0.3/0.6/0.9 | 概ね0.05(0.051とか0.049とか) |
| 軸方向 | 6 | 0.3/0.6/0.9 | 概ね0.05(0.051とか0.049とか) |
| 軸方向 | 8 | 0.3/0.6/0.9 | 概ね0.05(0.051とか0.049とか) |
| せん断方向 | 6 | 0.3/0.6/0.9 | 0.05/0.045/0.05 |
| パターン | 組み合わせ | せん断方向の結果 | 軸方向の結果 |
| ① | 2Hz+固有振動数を同時に1sec | 2Hzのみのグラフになる(共振しない) | せん断と同様 |
| ② | 2Hz(0~0.5sec)+固有振動数(0.5~1.0sec) | 0.5~1.0secで共振しないで減衰 | 〃 |
| ③ | 固有振動数(0.5~1.0sec)+2Hz(0.5~1.0sec) | ほとんど振動せず0.5~1.0secで2Hz振動 | 〃 |
| X非共振[2Hz] | 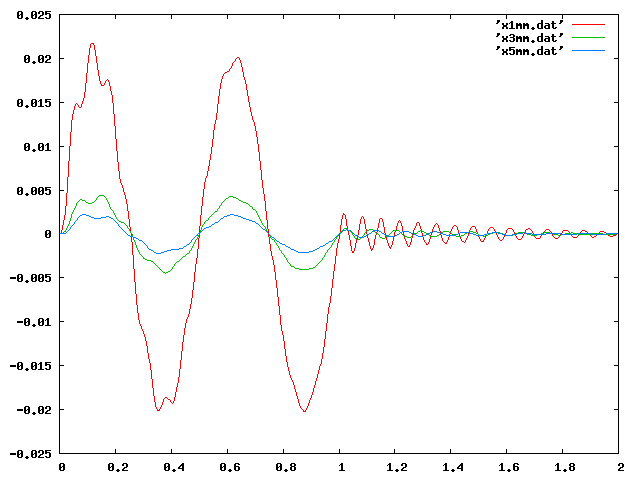 |
| Z 〃 | 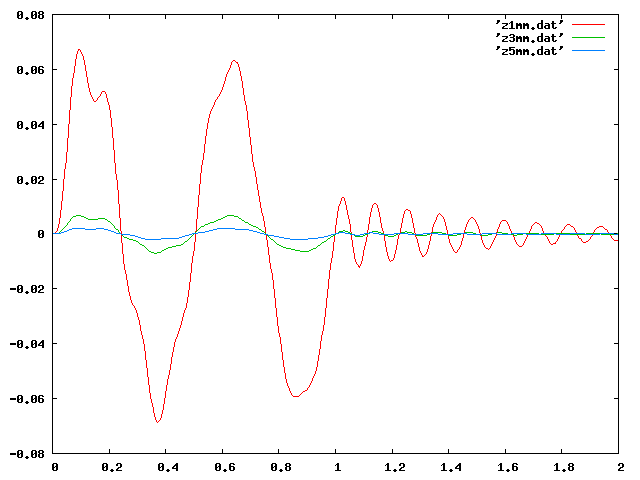 |
| X共振[9.46〜15.14Hz] | 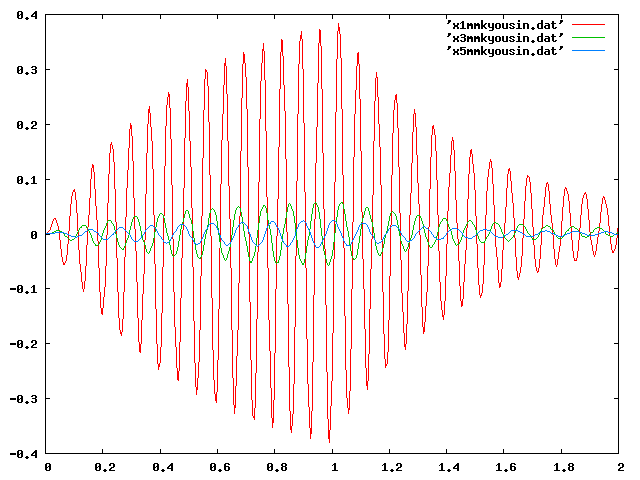 |
| Z共振[8.77〜9.63Hz] | 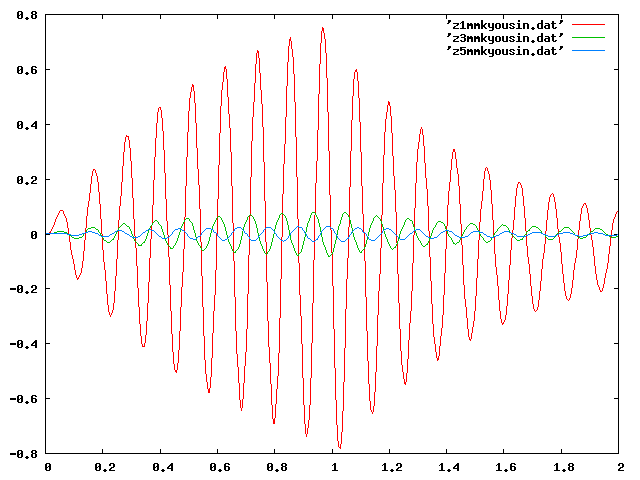 |
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/shuuha44.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/shuuha66.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/shuuha88.inp
XYZfree状態だとせん断方向の荷重に対する変形が、回転で出ている可能性がある ので荷重方向のみ自由(せん断はXYfree)にしてグラフを作ってみる。少々手間だが、 減衰もその都度ζ=0.03に合わせて設定する。…ただし、この条件だと固有振動数は 上がってしまう。実際は荷重方向のみに動くわけではないので境界条件をなくしたい …が変形が固有モードに依存してしまうので実際よりも高めの振動数になってしまう。
(続)と同様に、初期高さが低いほどせん断に強く、高いほど軸圧縮に強い結果となった。
| せん断 | 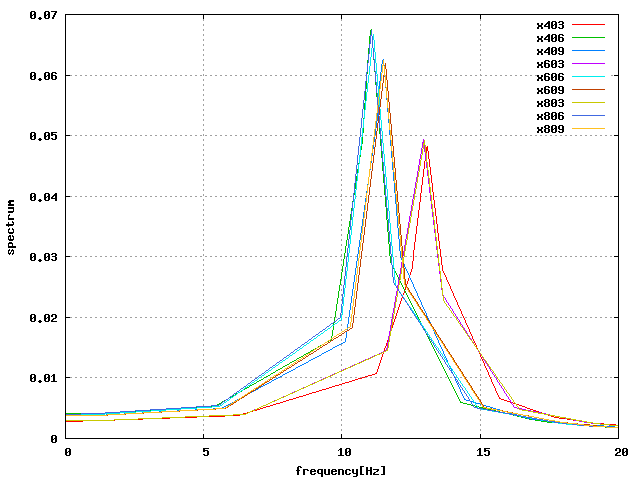 |
| 軸方向 | 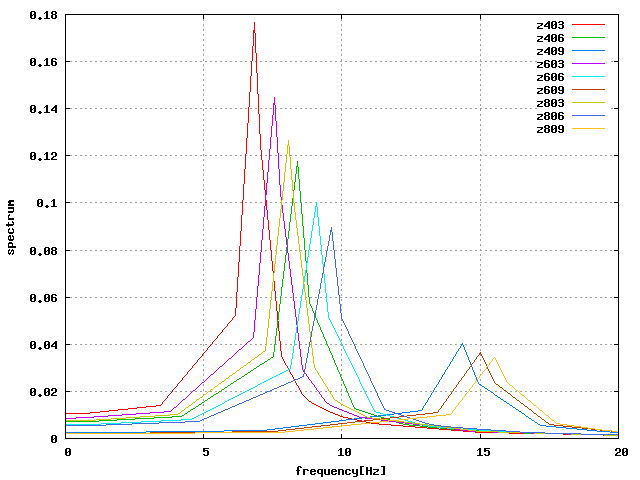 |
周波数応答解析中に不吉なエラーが表示された。 *ERROR: 1-D or 2-D elements cannot be used in a modal dynamic calculation BEAM・SHELL要素ではモード解析が使えない? ↑で一応解決! ちなみに*MODAL DYNAMIC では表示されなかった。なぜ*STEADY STATE DYNAMICS で表示?
分かりづらいので一応分けたグラフも作成。 0.3と0.6で2回山ができている周波数は、その振動系の二次モードである。
| せん断 | 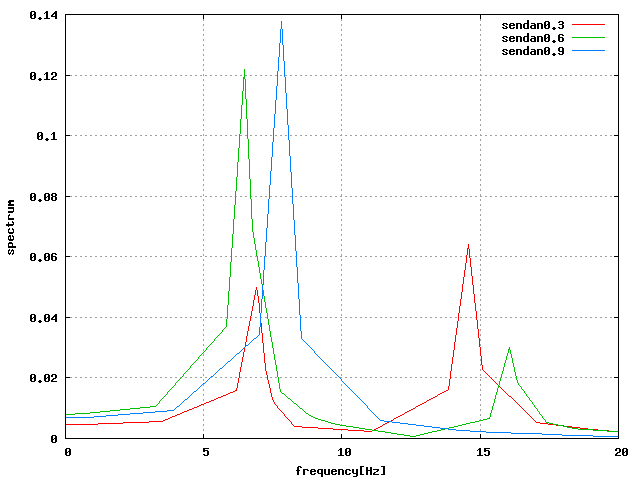 |
| 軸圧縮 | 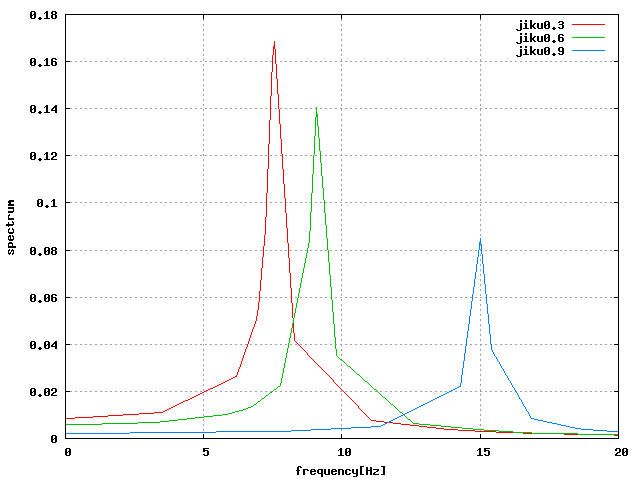 |
| 長周期地震動 | 周期が1~2秒以上[1Hz以下]。高層建造物に大きな被害が出る。 |
| 短周期地震動 | 周期が0.3秒以下[3Hz以上]。中・低層建造物に被害が出る。 |
免震について調べていたところ、構造物に対する免震対策は固有振動数を 高周波にするのではなく、短周波にして長周期化するのが基本だと今更知った。 理由は、短周期の地震は変位が小さく、被害はそれほど大きくならないが、 加速度が大きいから。一方、長周期の地震は加速度が小さいが、変位が大きい。 人が揺れを強く感じるのは短周期の地震だが、実際に大きな被害をもたらすのは 長周期の地震であることが問題で、せん断方向の剛性を下げて、あえて動かし、 ダンパーを利用して減衰させる。
表層が軟弱地盤であったり、震源がプレート間の場合、長周期地震動になる。 反対に表層が固い地盤や震源がプレートの深い位置だと短周期地震動になる。
※これまで、共振しなければ高周波であるほど良いと思っていたが、 免震支承として用いるのであれば、長周期化を考えるべきか?今の解析方法だと、 長周期化する方法が、①分割数を減らすか②設計反力を上げるしかない。 長周期化はやりすぎるとよくないらしく、1.5秒程度が妥当らしい。 また、軟弱地盤では逆効果になる可能性がある。
◆積層ゴム支承の中に鉛プラグを入れているが、なぜ鉛なのか? 他の金属が100℃超なのに対して、鉛は20℃で再結晶化するので、また、 塑性によってエネルギーを吸収できるかららしい。あくまで蛇腹のみで 機能分離型免震支承とする場合、ダンパーは中間発表の図のように、 蛇腹折りを横にする方法が良いと思う。 (軸圧縮モードとなるので、初期高さは高い方が良いのだろうか?)
| 周波数応答 | 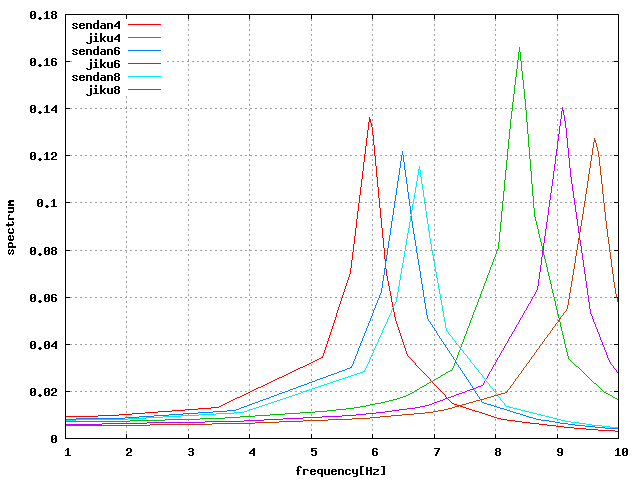 |
せん断方向も比較してみたが、やはり荷重方向に近いモード(せん断は1次)で 解析されており、共振振動数もそれに近いものになっている。
| 軸圧縮(Z):周4_8.38Hz | 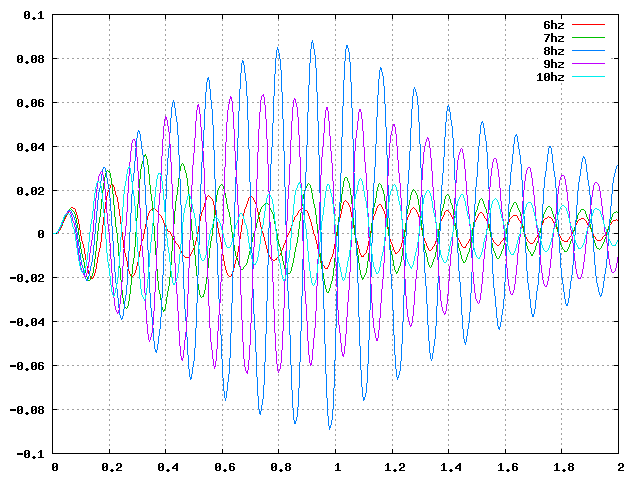 |
| 軸圧縮(Z):周6_9.08Hz | 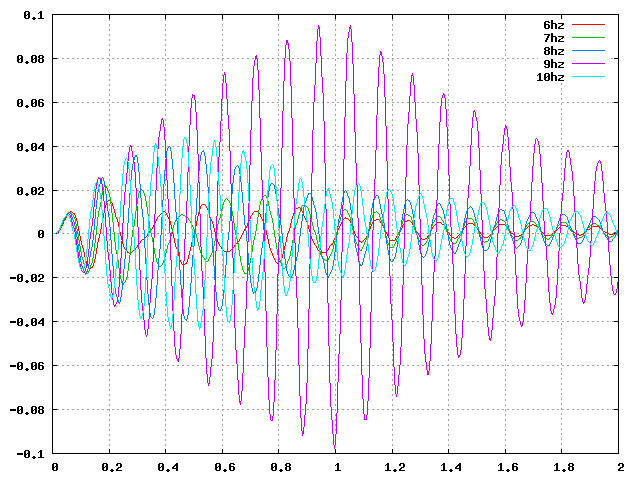 |
| 軸圧縮(Z):周8_9.61Hz | 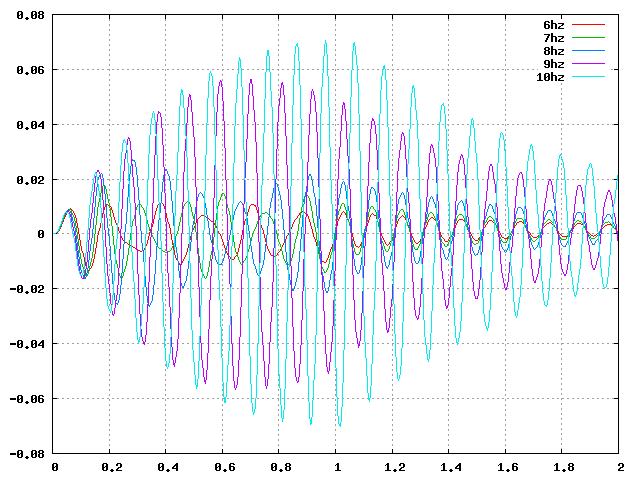 |
| せん断(X):周4_5.95Hz | 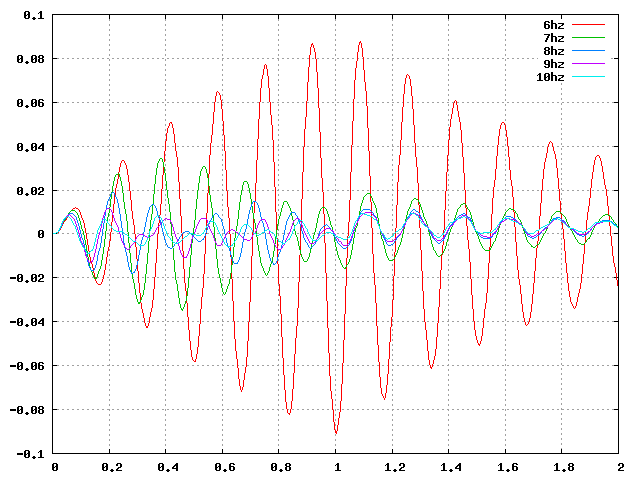 |
| せん断(X):周6_6.49Hz | 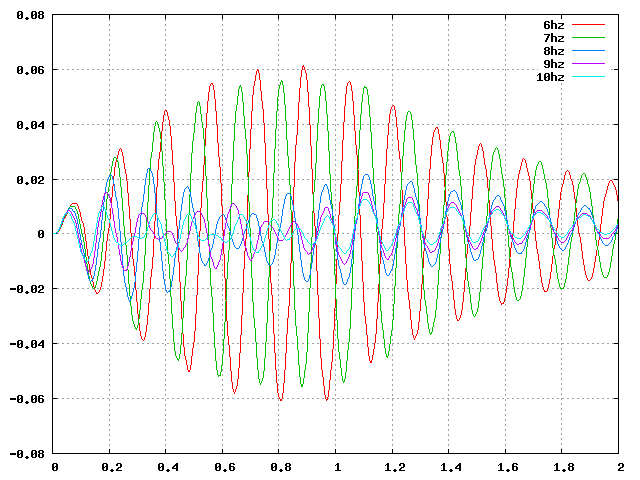 |
| せん断(X):周8_6.76Hz | 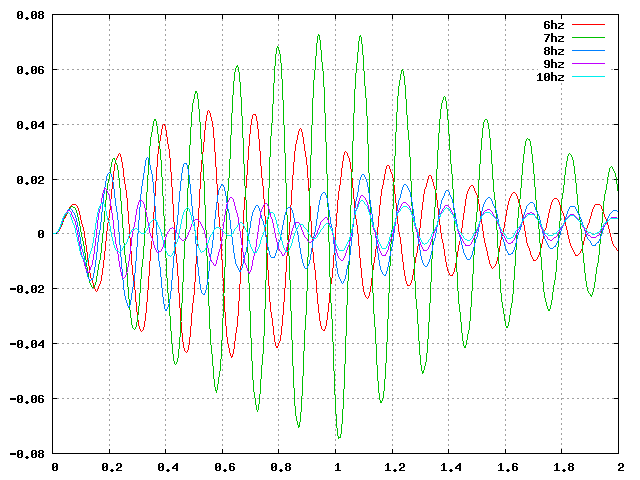 |
| 周6_XZ載荷 | 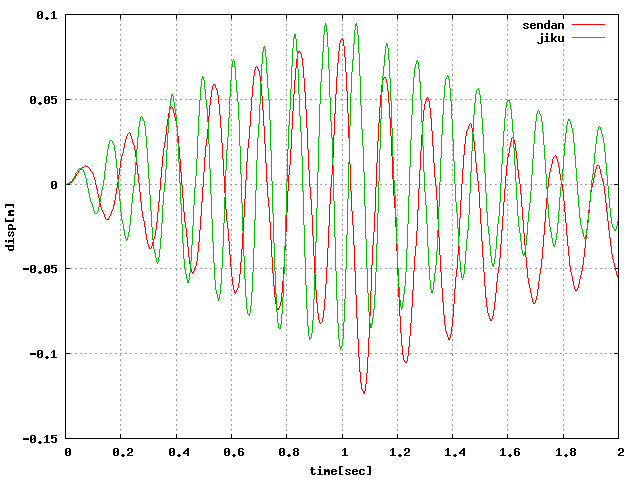 |
| 軸圧縮(Z):周4 | 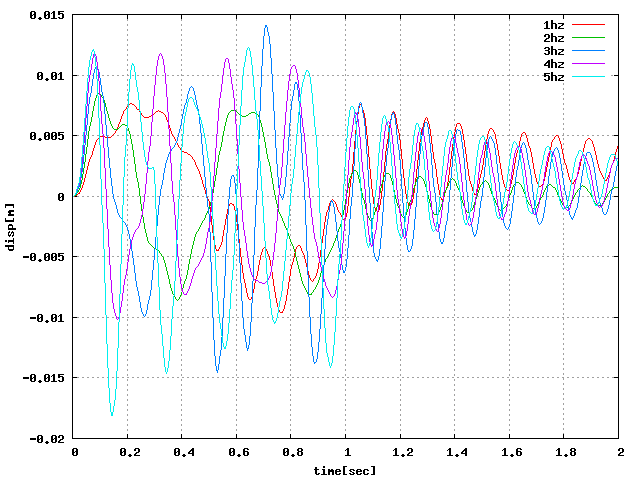 |
| 軸圧縮(Z):周6 | 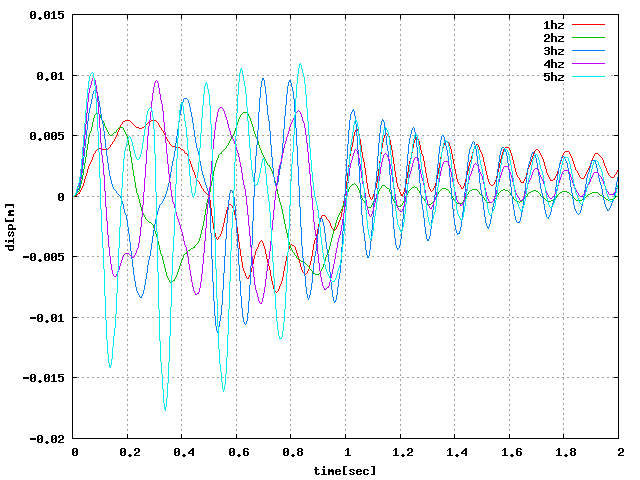 |
| 軸圧縮(Z):周8 | 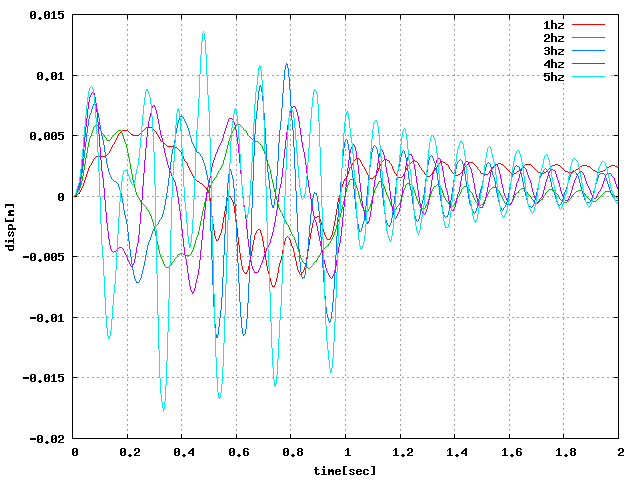 |
| せん断(X):周4 | 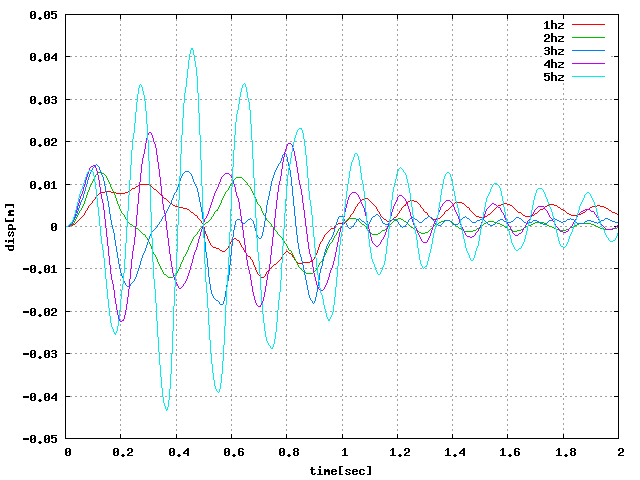 |
| せん断(X):周6 | 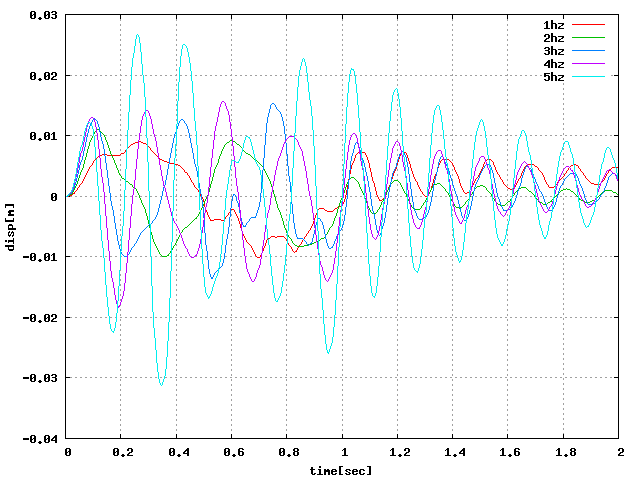 |
| せん断(X):周8 | 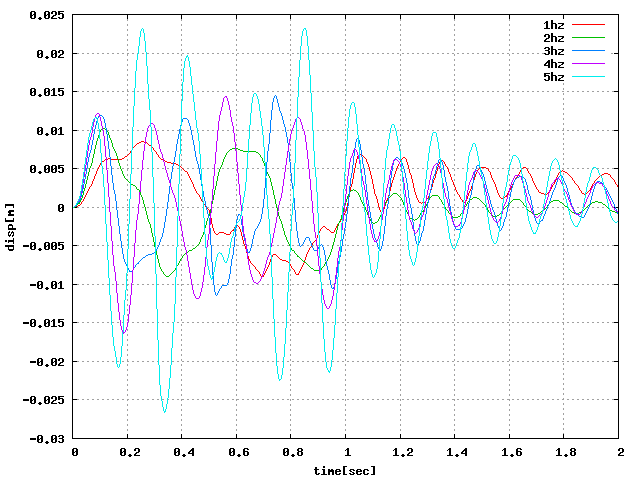 |
| せん断・軸圧縮 | 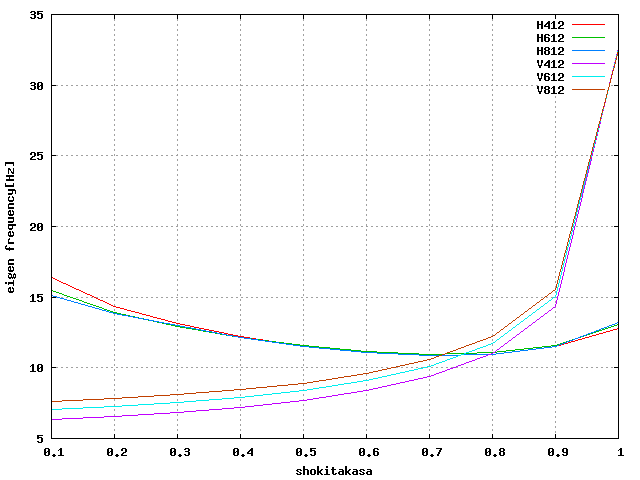 |
| ねじれ・回転 | 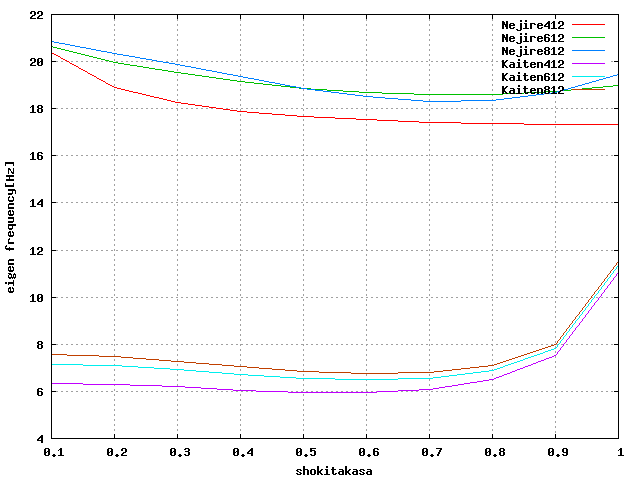 |
HARDENING=ISOTROPIC 等方硬化-バウシンガー効果を考慮していない HARDENING=KINEMATIC 移動硬化-バウシンガー効果を考慮している バウシンガー効果とは、一度引張りをかけて塑性変形させた後、圧縮をかけると、 圧縮側で降伏応力が低下してしまう現象。 等方硬化は移動硬化に比べて計算量が少なくすむので、一度の解析で変形方向が 逆転しなければ、等方硬化で十分。 逆に言うと、一度の解析で変形方向が逆転する場合は、移動硬化 (もしくは移動硬化と等方硬化の間の混合硬化)を使用したほうが、現実とよく合う。↑の理由より振動解析には移動硬化を使いたい。 なぜか[*PLASTIC]だとセグメンテーション違反になるのに、 [*DEFORMATION PLASTICITY]だと解析できる。移動硬化で解析を始めてくれたが、 1時間以上経っても終わらない…解析に時間がかかるものなのか? ccx2.3 でもスタートしたが一向に進まず固有値解析で止まっている →数時間経っても終わらないため、別の方法を探す。→どうにもエラーが消えず、 解析ができない。ソリッド片持ち梁でもセグメンテーション違反になった。
| XY(XYZfree) |  |
| XZ(XYZfree) |  |
| YZ(XYZfree) |  |
ということで…周6分割で試してみる。 周6と8は固有値解析からモードの出方を確認したところ同様の結果になる模様。 周4とは異なり、周6と8はX・Yの変位が全く同じに出たのでグラフは直線になった。 回転荷重はかけられない模様…周期荷重の設定をXY方向で変えて、 円のような荷重をかければ回転っぽくなるだろうか?
| XY(XYZfree) |  |
| XZ(XYZfree) |  |
| YZ(XYZfree) |  |
ちなみに200kNで9.41Hz。10Hzを基準とすれば、周4分割は約200kNが限界か? 周や高さ分割を増やせば、固有振動数は上がるが…500kNに対して 周6で6.5Hz・周8で6.8Hz程度だった。
BEAM要素による拘束部分の体積を求める 断面を矩形として、円周70cm・厚さ3mmなので0.003^2×0.7[m^3]が体積V 500kN/9.8[m/sec^2] = 51020[kg]/体積 V = 密度 ρ →*DENSITYに設定 地震時の揺れの大きさは加速度gal=[cm/sec^2]や速度kine=[cm/sec]で表される。 震度6を超える地震では加速度が2000galを超える。(東日本大震災では3000超) 2000gal=20[m/sec^2] f=ma より f=51020[kg]×20[m/sec^2]=約1MN
構造物の場合、通常は 0<ζ<0.1 であり、弾性域では 0.02<ζ<0.05 であるようで、 そこまで減衰は大きくないようだ。とりあえず減衰は弾性域の値を 使用して解析していく。(最も影響の大きい減衰は履歴減衰)
SUS304ステンレスはだいたい1kg=400円。ちなみに鋼材は1kg=100円ほど。 質量だけで換算すると周:70cm 高:20cm 厚:3mm より 1344円。 プレス加工はできるかわからないので費用は不明。 ゴムは高減衰・超高減衰になると値段が上がるはず… 支承一個当りの単価は鋼製支承より高いようだが、実際いくらか?
周8の場合が一番多く確認できたので、ひとつにまとめてみた。軸方向圧縮は 10000~15000としていたがグラフが比較しづらいのでもう少し下げてプロットした。
| H(せん断)V(軸圧)C(回転) | 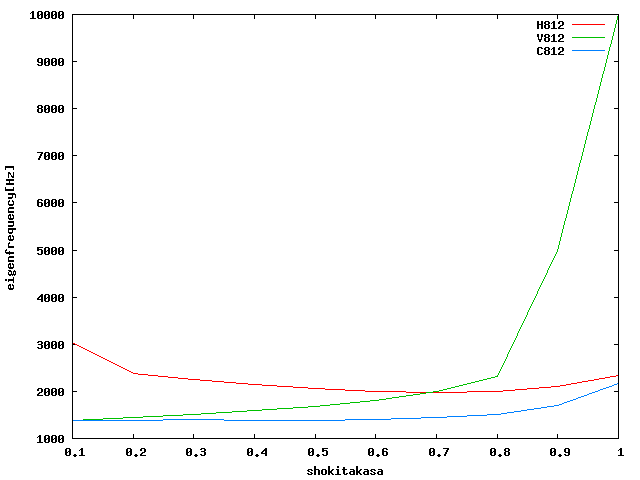 |
| せん断は周4のh1.0が確認できなかったので1600Hzで止まっている。 |
| 軸方向圧縮は周468でh0.9及びh1.0が8000Hzほどまで確認できなかったので10000~15000Hzに統一した。 |
| 回転は周8を除く周46でh1.0が確認できなかったので周8を参考にして同程度上げた。 |
↓以上、変形モードが微妙に違うようなものを除いて、 ある程度値を予想する形でグラフを作成してみた。
| せん断 | 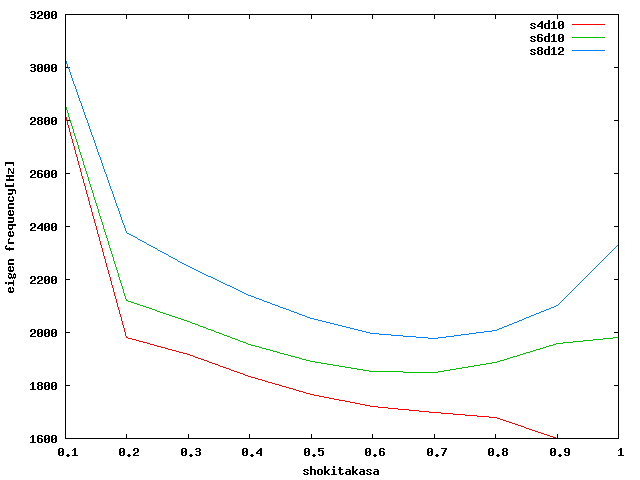 |
| 軸方向圧縮 | 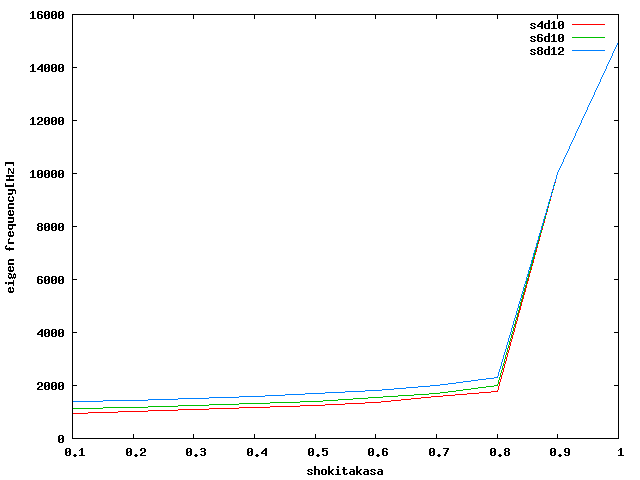 |
| 回転 | 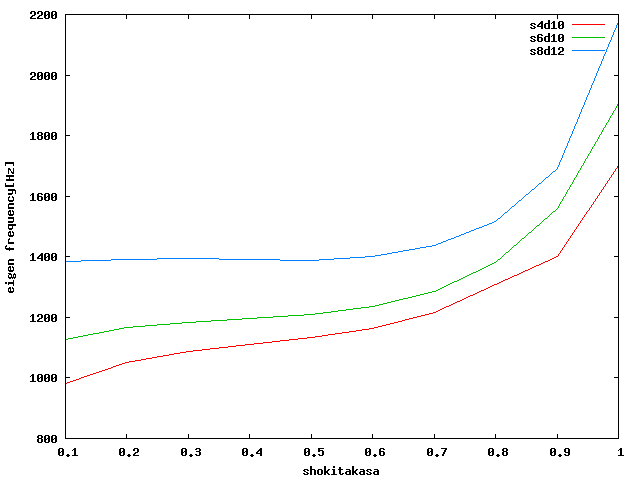 |
500kNになるようにBEAM拘束部分の体積に対して密度を設定したら、 固有振動数が5Hzまで下がった。この状態で2Hzのsin波を1secかけると、 グラフは周期に依存しない形となり、0を基準に減衰振動した。 周方向や高さ方向分割数を変えて、支承の固有振動数が卓越周期に 近くならないようなモデルを探してみる。 (※BEAM拘束部分の密度が以上に大きいのは不自然だが、モデルの大きさを変えると ソリッド要素を載せたものをまたinpファイル上で作らないといけないので 時間が足りない上に周68が比較できない。 後藤さんの言う一段目を薄くして硬化+密度大も試す)
| 開口部拘束なしの回転モード | 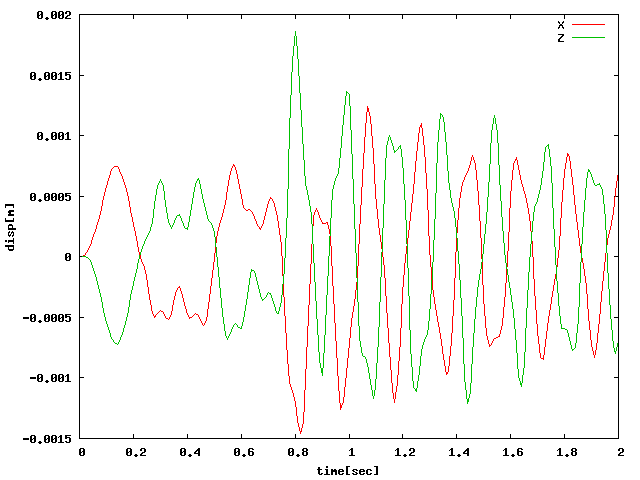 |
| モデル | 円周 | 高さ(折る前) | ヤング率 | ポアソン比 | 段数 | 周方向 |
| 70cm | 20cm | 200GPa | 0.3 | 12 | 4・6・8(+α?) |
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/senkou44.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/senkou66.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/senkou88.inp
モード解析では、一次モードしか解析できず固有振動数がすべてなので、 振動特性は[*FREQUENCY]の結果の延長線でしかない。しかも、 上にソリッド要素を載せることで固有値が大きく下がるため、 実際に使用する状態でないと大して意味がない? (今の状態でシミュレーションしたものを[巨大化or他の構造を足す]と 固有振動数は大きく変わるので特性も変わる。)
グラフの形が同じなら条件を変えて変位を比較しても、 剛性を比較しているだけで振動特性を比較していることにはならず、 動的解析の意味があまりない。また、荷重の周波数に依存することは 振動特性ではなく変位特性に思える。
片持ち梁(Solid)のように周期荷重に対して共振せずにグラフの形が 不規則になるような結果が出れば、時間--変位グラフに一定でない差が出るので 一応振動特性を見ていることにはなるが、それができていない。 (それすらもモデルによるが)
パルス荷重をかけて、時間刻みをかなり小さくすれば固有周期で 自由もしくは減衰振動していることが確認できるが、周期的な荷重に対して 変位がどう変わるかを見ない限りは、剛性比較になっていると思う…… のでどうにかして荷重の周波数に依存しないグラフを作りたいが、 モード解析(直接法もだが)だと蛇腹構造の動きが 片持ち梁にもバネにもなっていないことが問題だ。
| 回転モード | 載荷点拘束なしX載荷(周方向468) |
| X | 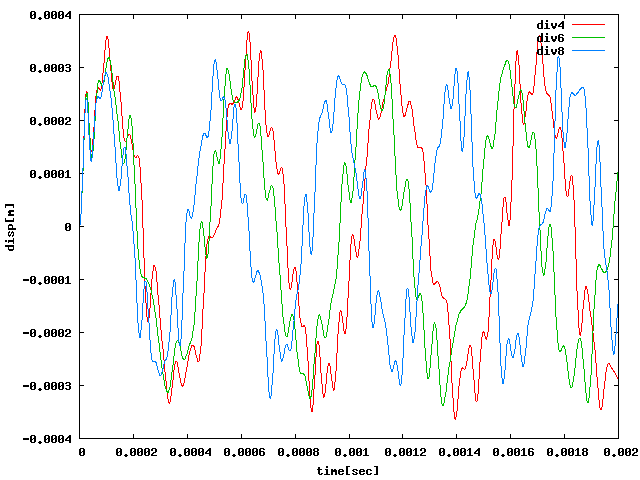 |
| Z | 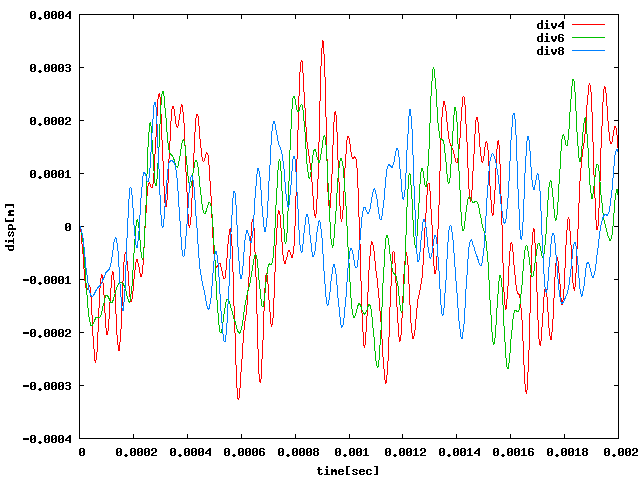 |
●一瞬の励振による自由振動では0を基準として限られた範囲で振動するが、 それ以上に周期荷重などを加えて強制的に振動(というより変位)させると、 基準からずれて振動してしまうため、グラフの形がおかしくなるのではないか? (赤4角・緑6角・青8角)
| X | 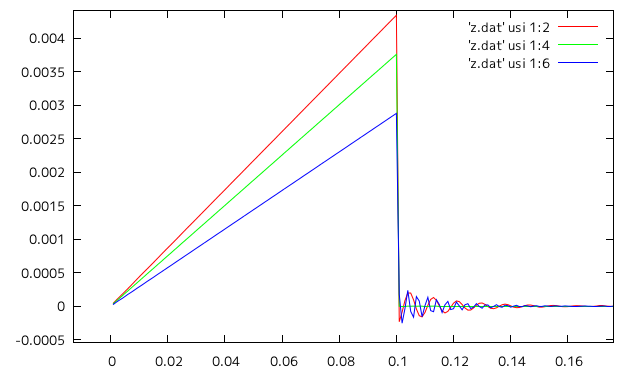 |
| Z | 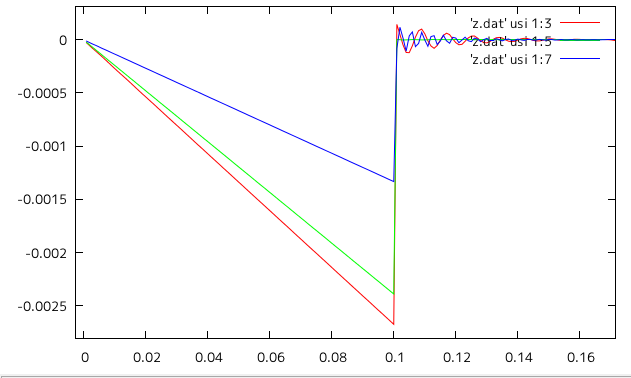 |
| Y | 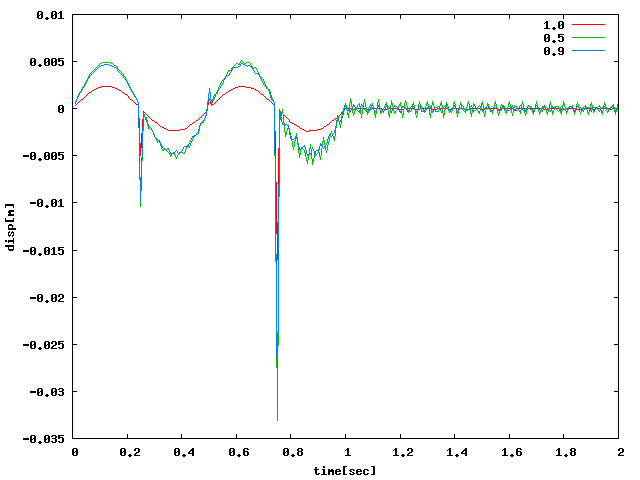 |
| Z | 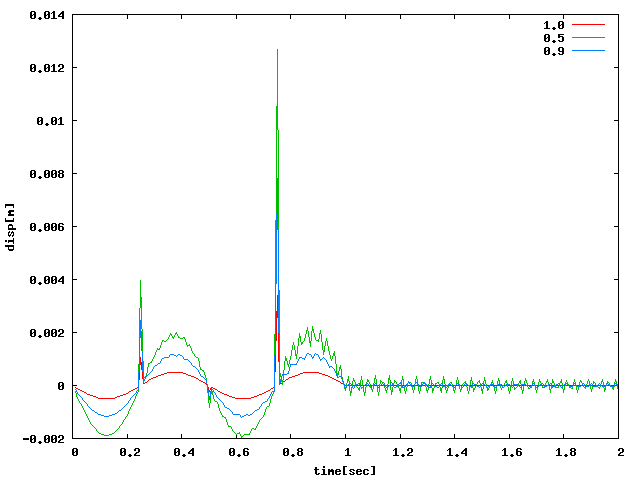 |
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/sol4.inp
①最小時間ステップよりも前に荷重を入力すると解析結果が0になる場合がある 結果を見る時間ステップを1.d-2にして最初に荷重をかける時間を1.d0とかにすると たとえ5.d0までと設定していても全ステップの変位が0になることがあった。 モード解析では、一次固有モードをもとにステップごとの変位を重ね合わせで 計算しているため、荷重の入力がない部分があると計算できず後のステップでも 0になってしまうのではないか。 ②時間ステップを変えることで振動していたグラフが負の一定値に収束する 時間ステップを細かくしたら、負の一定値に収束するのは不自然だ。 より細かく点をとったなら滑らかになるか、複雑な形になると思う。 時間の刻みを細かくし過ぎると変形を計算できず、一定になっている可能性がある。
| P波とS波の同時入力 | MODAL DYNAMIC | 2Hzと3000Hzで入力したが変わらず… |
| →他にも複数の荷重を多方向+違う条件で試したが形は変わらず | ||
| 周波数応答解析 | STEADY STATE DYNAMICS | 卓越したのは固有周期(3000Hz)付近だった…1~10Hzの範囲で卓越するかを確認したい |
| →ソリッド要素を載せて固有振動数が下がるか? | 下がったが形は変わらず。 | |
| 直接積分法 | DYNAMIC | 解析途中でエラー |
| →陰解法・陽解法ともにエラーが… | 陰解法でモード解析と同様の結果になった |
↑CLOADを追加してかけただけなので入力モードはありません。 グラフの形が変わるかと思いつきで試しただけで詳しくは調べていません。
| X | 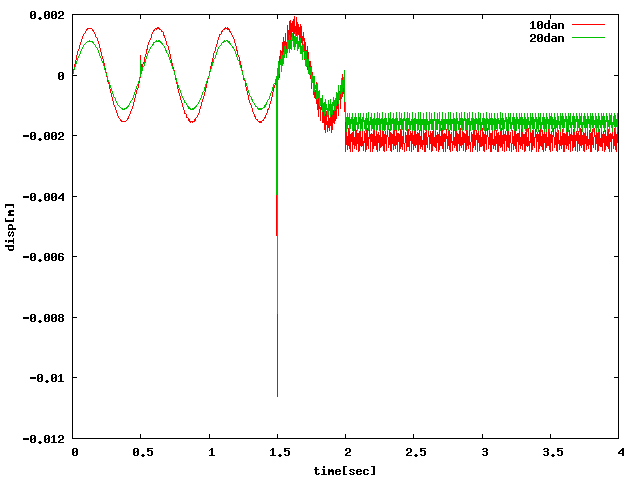 |
| Y | 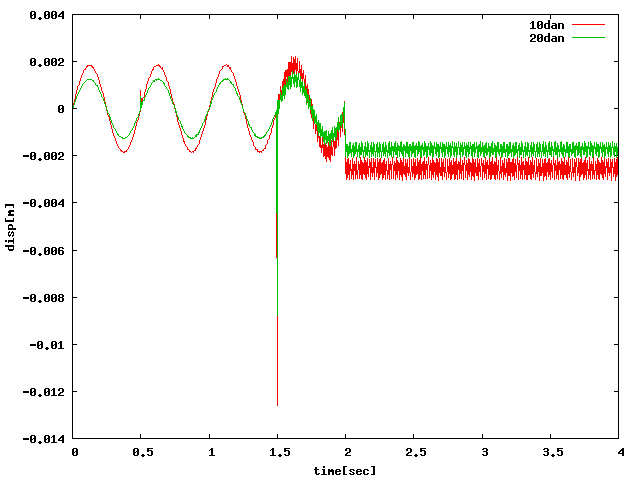 |
| Z | 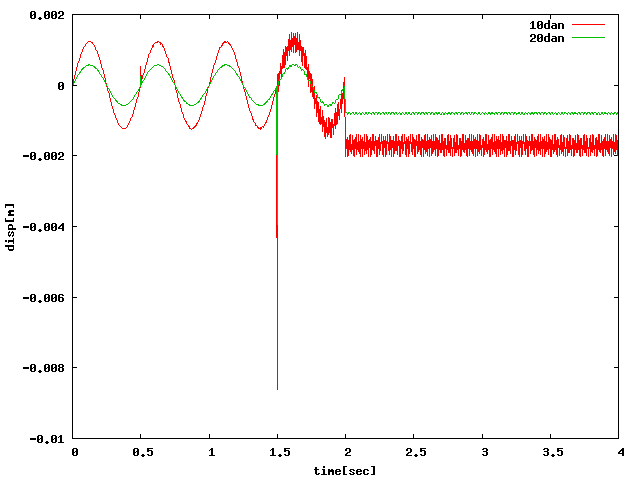 |
BEAM32要素で載荷点を1周してヤング率を大幅に上げたら一段目を硬化したものと ほぼ同じ結果が得られた。一段目の要素を硬くした不自然な条件でなくても BEAM要素で拘束することで載荷点の変位は一定に出力できる。しかし、 グラフに関してはすべての方法で負の一定値に収束するので対策が必要。 (SPRINGAでは設定が分からず色々変えても「剛性増加なしの変位」に 近い値のばらつきが出た。)……下のサンプルはアルミ缶大のもの。
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/kousoku4.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/kousoku6.inp
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/kousoku8.inp
| Z |  |
| y | 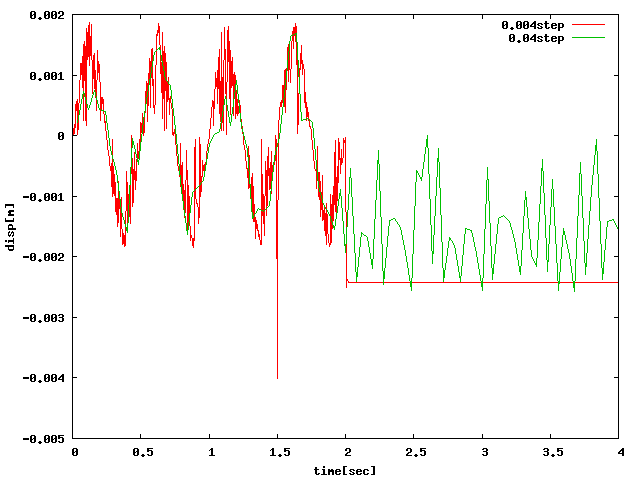 |
5mmにした場合に、荷重がなくなった後に負の一定値になってしまうものがあり、 全弾性なので原因不明…。また、各方向において厚さを1mmにして解析すると、 以前に挙げたエラーによって最終ステップまで結果が出力されない場合があり、 特に極端であったY方向のみ1mm→2mmとして解析した。
| X | 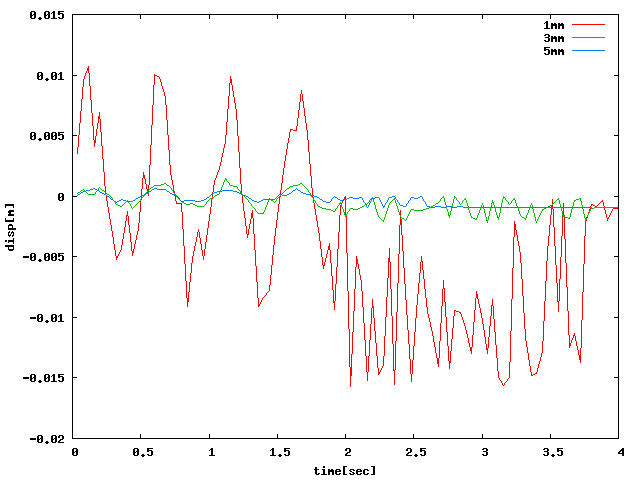 |
| Y | 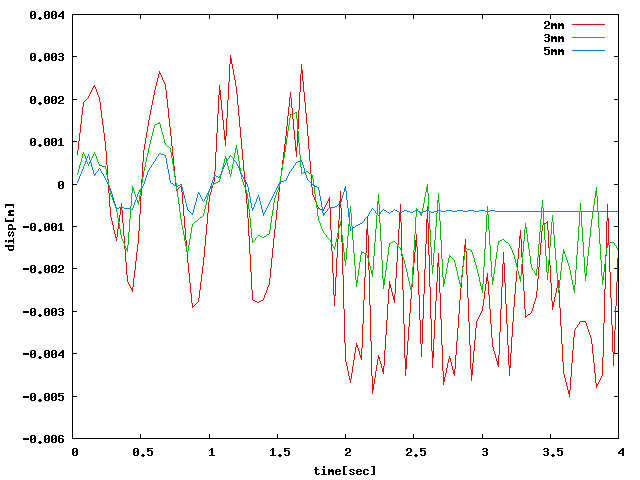 |
| Z | 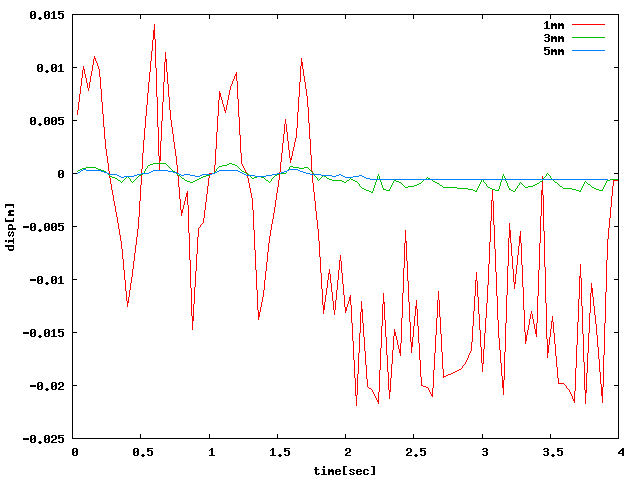 |
XYZ方向すべてに関して、hutaもしくはheibanの方が荷重がなくなった後も 振動していて(※減衰の設定はしていないので2sec以降は定常波形になるはず)、 振動解析っぽいグラフになったが、負の範囲で振動している問題が解決していない… 周方向が6・8分割であってもおそらく同様の結果になると思う。 (※ccx2.3であっても4点載荷であればほぼ同じ解析結果だった)
| X | 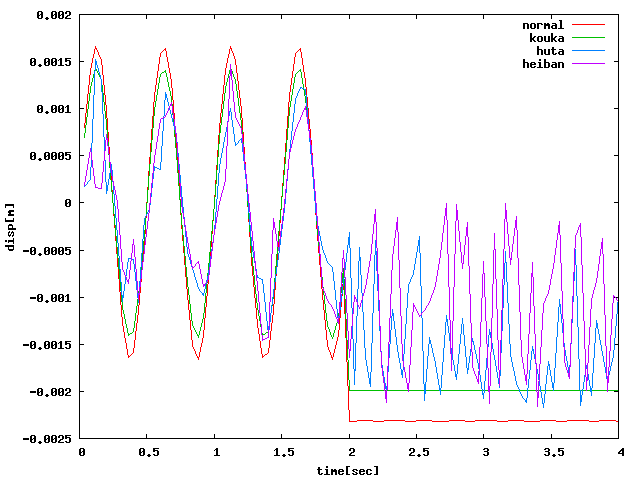 |
| Y | 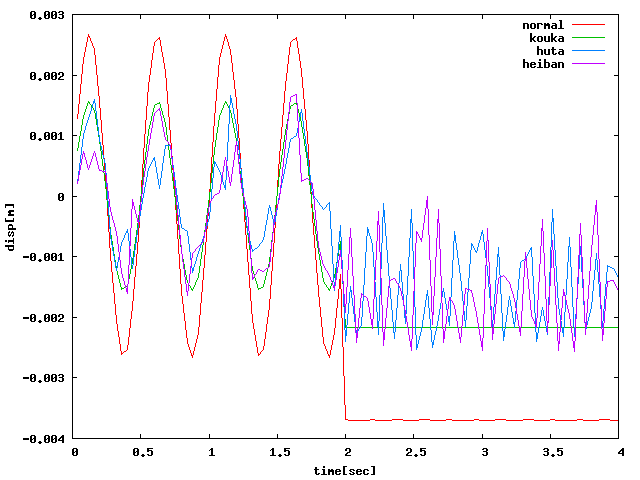 |
| Z | 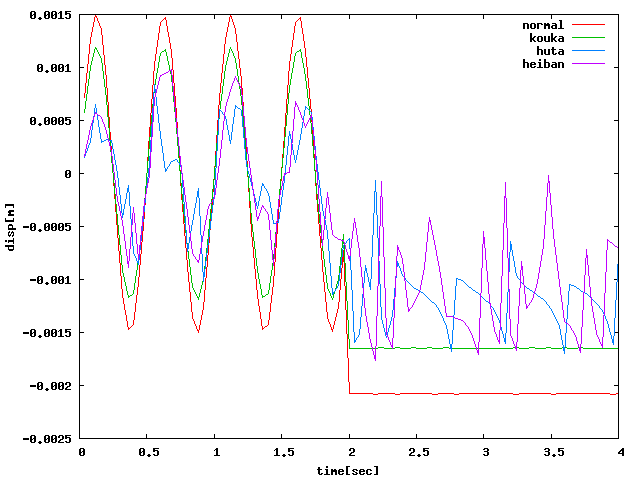 |
| 分割数(X*Y*Z) | 理論値[mm] | calculix[mm] | 相対誤差(%) |
| 2*2*10 | 3.333 | 1.2847 | 61.46 |
| 4*4*50 | 3.333 | 3.0920 | 7.23 |
| 8*8*100 | おそらく3%以下で一致する |
全要素をEallなど一律でセットしている状態で、DLOADでEallの面を指定してしまうと 分割したすべての要素の面に荷重をかけてしまう。 構造力学における等分布荷重の問題は梁上面に載荷しているため、 上面を含む要素のセットに対してDLOADを載荷しなければならない。 inpファイルを書き換えて解析すると表の結果となった。
一次要素(C3D8)の場合、ロッキングにより剛性が高く評価され易いため、 理論値よりも変位が小さくなる。要素分割数を十分に増やすことで、 理論値に近づけることが可能だが、より少ない要素数で高精度を得たければ、 二次要素(C3D20)を用いた方が良い。二次要素であれば、 断面2×2・軸10であってもほぼ理論値と一致する。(テトラ要素でどうなるかは不明)
ロッキングについて[株式会社アライドエンジニアリング] (http://www.alde.co.jp/advc/memo/locking/index.html)
S6・S8要素はともに二次要素だが解析結果には大きな違いが出た。 (※DLOADでは自重以外は弱軸方向にしか載荷できない)
| ELEMENT | 分割数(X*Z) | 荷重[MPa] | 理論値[mm] | calculix[mm] | 相対誤差(%) |
| S6 | 10*10 | 0.001 | 2.08332 | 0.079099~0.075931 | 論外 |
| S8 | 2*5 | 0.001 | 2.08332 | 1.8510 | 11.15 |
| S8 | 2*5 | 自重[強軸] | 1.37813e-4 | 1.4097e-4 | 2.29 |
| S8 | 2*5 | 自重[弱軸] | 5.5125e-2 | 4.8978e-2 | 11.15 |
S6の場合、自重による変位であっても理論値の1/10ほどの変位だったため、 表には載せていない。S6要素で解析した結果、ロッキングにしては変位が大きく減り、 理論値より大幅に小さくなった。S8では分割数が少なくても、 許容範囲の変位が出ていて、自重による変位では強軸方向の誤差はわずかだった。
したがって、DLOADでの解析には四角形二次要素が適していることが分かった。 S6のような三角形二次要素だとロッキングに似た剛性の過大評価が生じている 可能性があり、変位結果も自由端節点で一定でなく角から角へ減少(増大)しているため 偏心しているのかもしれない。
inpファイルは頭が[*HEADING]で始まる以外はほぼ同じ状態で使用可能。 要素の名称が異なるため、使用する前に調べたほうが良い。(S6→STRI65/S8→S8R ?)
(余談)S8にRをつけると低減積分要素になり、荷重の分布がおかしくなったりするため、 普通に解析する場合には用いず、用いる場合にはそれなりの工夫が必要らしい。 しかし、ABAQUSの三角形二次要素はSTRI65しかない模様…
周方向4分割であれば、inpファイル上で新たに節点を追加して、 薄板を載せることは容易だが、開口部の形が複雑になる6・8分割になると、 載荷点をすべて含むように薄板を載せるのにかなりの時間がかかってしまう。 →salomeでできるか?
変位に違いはあるが、載荷点を含む要素を硬化した状態で、 各周方向分割の角にCLOADで載荷することで、XYZ方向それぞれに対して、 一定の変位を出力することが可能となった。周方向で比較したい場合には、 こちらの方法が分割数などのモデルを変更した場合にも、 すぐに解析可能であるので良いかもしれない。また、ccx2.3でも一定となるため 「解析結果として」は正しく出力できる。 (蓋や薄板載荷はccx2.3ではエラーで1ステップのみ)
※「硬化していないただの蛇腹折り構造」に4点載荷した場合は完全に一定ではないが、 ある程度一定の値が出力できる。(最大で1の差[乗数に関係なく])
固有値解析の結果も同様で[*FREQUENCY]による結果に違いは見られなかった。
モード解析の結果は以下のグラフのようになり、 1.7に比べ2.3の方がグラフが粗くなった。Y方向に載荷し、 X_Y_Z方向変位を順に1:2_1:3_1:4のグラフに表しているが、 datファイルでの値も微妙に違いグラフの形も変わった。
| 1.7 | 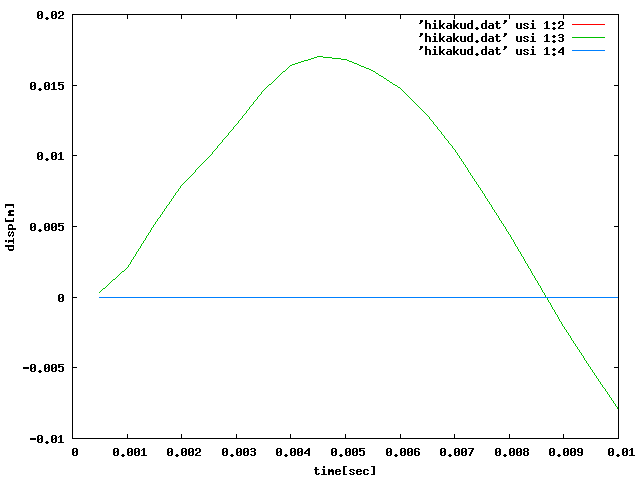 |
| 2.3 | 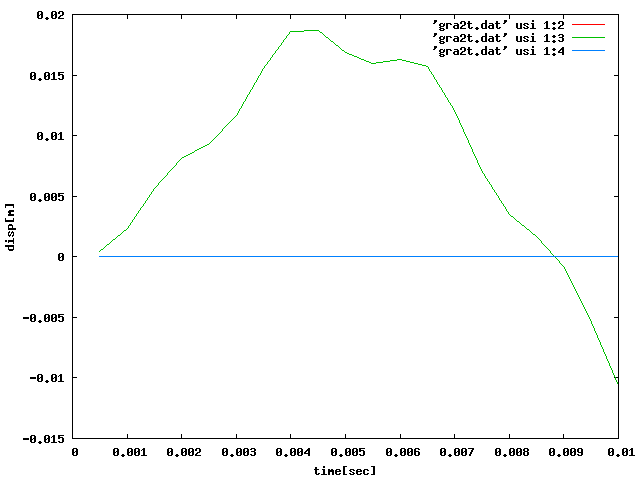 |
薄板を載せた蛇腹折りモード解析でエラーが表示され、変位が全て0となった。
*WARNING: 1-D or 2-D elements may cause problems in modal dynamic calculations
ensure that point loads defined in a *MODAL DYNAMIC step
and applied to nodes belonging to 1-D or 2-D elements have been
applied to the same nodes in the preceding FREQUENCY step with
magnitude zero; look at example shellf.inp for a guideline.
Composing the dynamic response from the eigenmodes
*WARNING in noelfiles: parameter not recognized:
POSITION=AVERAGEDATNODES
*WARNING in the input deck. Card image:
*ELFILE,POSITION=AVERAGEDATNODES
固有値解析の結果は同じだったが、モード解析の結果で違いが出た。 載荷点を含む要素を硬化したものでは、X方向変位が一定であったのがバラバラになり、 完全に固定しているはずのZ・Y方向の変位が0でない点がいくつか表れた。 変位もX方向の最大変位に近いため解析結果がおかしい。
→載荷点を含む要素を硬化して、4点に載荷したものはccx2.3であっても 一定の変位が出力できた。薄板の場合も恐らく同様の結果となる可能性が高い。
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/heiban4.inp
開口部中心から載荷点までの各平面座標(X,Y)を2倍して載荷点を含みかつ開口部を はみ出すように薄板を載荷して解析したが、板の角4点に載荷しても載荷点の変位は 一定にならなかった。また、板の中心と角4点に載荷してもバラバラだった。なお、 蓋をした場合と同じく載荷点の角4点に載荷した場合は一定となった。 水平方向に関しても載荷点の角4点載荷以外では変位が一定にはならなかった。
http://www.str.ce.akita-u.ac.jp/~gotouhan/sudo/sample_file/huta4.inp
①角4点に載荷→水平・鉛直方向ともに完全に一定の値を出力できた。 気になることは、③のように硬化要素に水平方向の荷重をかけた場合と比べて ①の方が変位が小さくなること。
②載荷点を除いて薄板の節点だけに載荷 →全く一定にならず、正負にバラバラに変位した。
③載荷点を含む要素を硬化して、一段目と二段目の境目に載荷 →境目に分布させた場合はバラバラだったが、 境目の中心1点にかけた場合は、大まかにだが一定の値が得られた。
よって、薄板を載せた状態で4点載荷をすれば、 XYZ方向全ての変位がモード解析で一定となる。
cgxで要素番号と節点番号を出力して載荷点の番号を確認。
表示する方法は以下の通り
cgx_1.7 ***.frd または cgx_1.7 -c ***.inp
(※cgxのウィンドウが手前に表示された状態で)
plot ea all
plus na all
載荷点を通るような薄板要素をinpファイルを書き換えることで加え、解析する。
①まず最も簡単に薄板をつくる。 周方向4分割・高さ10分割の蛇腹折りの載荷点の4つの角にあたる点を指定して、 S8要素で薄板を作ったが、モード解析の途中でエラーが表示され解析できなかった。 薄板要素は極端に小さくないはずだがエラーが出た。
*INFO in gen3dnor: in some nodes opposite normals are defined *ERROR in gen3dnor: size of estimated shell normal is smaller than 1.e-10②S6要素を2つ組み合わせて薄板をつくるために載荷点を含む4辺の中点を確認。 開口部中心に新たに点を設定し、3点を共有したS6要素を作ったが、 ①と同様のエラーが出た。
③載荷点を全て含むようにS8要素で薄板を載せて解析したところ、 解析可能だったがモード解析で別のエラーが表示された。このため、 変位は1ステップしか確認できなかったが、その値はDLOADをかけた状態で 完全に一定となった。「CLOADで37点(載荷点24+追加13)に分布」させても 一定とはならなかったため、「薄板+DLOAD」は鉛直方向のみで有効であることを確認。 問題は荷重の設定と変位の理論値が片持ち梁で一致していないため、 「どれだけの荷重に対してその変位が出ているか不明確」であること。 (なお、薄板の全節点に対して水平方向にCLOADをかけた場合、 変位がバラバラに表示された。)
*WARNING in subspace: ddeabm did not converge properly idid= -4 switch to routine ddebdf *ERROR in subspace: ddebdf did not converge properly idid= -1 *ERROR 以下は出ない場合もあり、その場合は全ステップ解析結果が出力できた。 DLOADの場合にエラー以下が出ることを確認。
問題点 ①片持ち梁だと変位に偏り(自由端での傾き)が生じてしまう。 要素が三角形であり、圧力が若干偏っていることが原因だと思われる。 ②圧力(鉛直方向にかけているにも関わらず、水平方向の変位が 鉛直の1/10か1/100と大きく出ることがあり、モデルの寸法と要素分割数によって 変わることがわかる。 解決策 ①変位の傾きは自由端における三角形要素の底辺部分が片側に分布しているために 生じると考えられ、梁をなるべく細長くすることで傾きを軽減できた。 ②水平方向の変位が大きく出るのは、細長くするほど影響が大きくなるようだが、 幅と長さの比を1:10ほどにすると概ね解決した。蛇腹折り…板を載せていないが、載荷点を含む硬化要素に載荷したところ、 鉛直方向において変位が一定となった。水平方向に関してはバラバラだったため、 今のところ鉛直方向に関してのみ有効だと思われる。
etc…DLOADにするとCLOADと同じ荷重をかけても変位が$10^{-3}$ほど小さく出た。 要素に対する圧力になるため、集中荷重よりも小さくなるが、たわみの理論値と 比較しても計算が一致しないため、荷重の設定を見直して精度を確認する必要がある。
塑性変形の可能性について…変位がパルス荷重の載荷方法が正のみであっても、 二度に分けてかけた時に、荷重がなくなった後の変位が負で一定となってしまった。 一度目の荷重によって固有振動し始めるところに新たに荷重が加わったことにより、 塑性変形が生じたことが原因かもしれない。←塑性はそもそも入っていないため、 別の要因がある。
6面体要素→面1:1234 面2:5876 面3:1562 面4:2673 面5:3784 面6:4851 4面体要素→面1:123 面2:142 面3:243 面4:341 くさび型要素→面1:123 面2:456 面3:1254 面4:2365 面5:3146 四角形平面の応力、平面ひずみと線対称要素→面1:12 面2:23 面3:34 面4:41 三角形平面の応力、平面ひずみと線対称要素→面1:12 面2:23 面3:31 梁要素→面1:1の(垂線)方向における圧力 面2:2の(垂線)方向における圧力★シェル要素の場合、載荷方法(そのシェルに対する垂線方向の圧力)が ただひとつなので面の番号付けは必要ない。
面荷重は分布荷重の種類ラベル$P_{x}$(xは面の番号)を用いて、 一様な圧力として入力される。よって、圧力荷重では荷重の大きさは正であり、 張力荷重では負である。一様でない圧力の場合は$P_{x}NU_{y}$のラベルを使用し、 ユーザーのサブルーチンdload.fが必要となる。ラベルは最大20文字まで設定できる。 この時、yは異なる一様でない荷重パターンの判別に使用される(最大16文字)。 一様でない荷重の代表的な例は静水圧である。(訳が下手)
etc…シェル要素では荷重方向が要素に対する垂直方向のみに限られるため、 片持ち梁の強軸方向や蛇腹の水平方向(鉛直方向も正しくはならない)に 載荷することができない。 プログラム上の設定は目次より[Calculixで新たに使用したオプション]参照
| ◆片持ち梁 | ①自由端中点のみに載荷で解析可(端の硬化は強軸・弱軸ともに無効) |
| ②周期・パルスに関係なく固有周期で振動(卓越周期[1Hz]では変位が若干負に傾いた) | |
| 問題1:分布荷重に対する出力変位が一定にならない原因を調べる必要がある | |
| ◆蛇腹折り | ①載荷点を含む要素の硬化→水平方向は概ね一定の変位(鉛直方向は失敗) |
| ②パルスでは固有振動するが、正負を含むと安定せず(正や負のみの範囲で振動する) | |
| 問題1:卓越周期の荷重に対して固有周期で解析結果を出す必要がある | |
| 問題2:鉛直方向および回転に対する解析ができるか試す必要がある | |
| 課題:鉛直方向に関しては薄板を自由端開口部に載せる必要性が高い |
◆エラー:荷重の設定と解析する時間間隔(ステップ数)によるのか、 周4分割のモデルを高さ分割を10→20にしたところ、 モード解析でセグメンテーション違反が出るようになった。 ただ荷重やステップによっては解析可能となることもあったが、 効率が悪いのでセグメンテーション違反にならない分割数で解析を進める。
→要素分割数が多いとエラー(セグメンテーション違反)が出やすくなるが、 周方向を10分割以上にすると、高さ10分割のモード解析において、 別のエラー(FREQUENCYの段階で *ERROR in u_calloc: error allocating memory →カロック関数におけるメモリ分配のエラー?容量の不足?)が生じることが わかっている。高さ方向を20分割にすると解消されることから、 周方向とのバランスが重要だと思われる。
| 解析可となる例 | 周方向分割 | 高さ方向分割 | エラー確認範囲 |
| 4 | 10 | 高さ2(モデルが正しく作れていない←cgx_1.7 -c ***.inpで確認) | |
| 6 | 10 | ||
| 8 | 12 | 高さ10(セグメンテーション違反) | |
| 10 | 16 | 高さ10~14(セグメンテーション違反) |
| パターン | 変更する点 | 結果 |
| 1 | アルミ缶程度にして解析 | ×前回までと同様の結果 |
| 2 | 分割数をできるだけ減らして解析 | ×高さ方向分割が少なすぎるとモード解析でエラー |
| 3 | 一点載荷もしくは三点載荷 | △自由端変位が概ね一定となる |
| 4 | 載荷点のヤング率を増大させる | ○数点を除いて変位が一定となる |
| 5 | 載荷点の上にヤング率の大きい板を乗せて解析 | ?↑4で代用 |
<datファイルで確認したいこと…載荷点の変位がすべて同じ値となる>
[方策1]:蛇腹折りに関しても片持ち梁と同様に、一点載荷が自由端変位を 一定にするのにある程度有効だった(蛇腹の場合には三点載荷でも可だった)。 [グラフ①から③は三点載荷で最大変位を示した節点について]
[方策2]:載荷点のヤング率を$10^6$して解析してみる。
周方向4分割・高さ方向10分割のモデルに対して分布荷重で解析したところ、 載荷点24点のうち5点を除く節点の変位がすべて同じ値となった。 載荷点を少なくする方法に比べ、節点の変位が(5点を除き)完全に一致しているので、 有効だと思われる。 問題の5点は変位が他と比べて極小なので、節に当たると思われる。
→XおよびY方向(水平)では一定の変位が確認できたが、 Z方向(鉛直)では節点によってばらつきが出た。 変形しやすい面ができてしまうため、鉛直方向に対して解析する場合は、 変形しない板を上に載せて荷重をかける必要があると思われる。
<グラフで確認したいこと…以下>
| 1 | 固有周期で振動するか? | →パルスでは成功。周期では荷重の振動数になる。 |
| 2 | 変位が異常に大きくならないか? | →周期およびパルスでマイナスを含むと失敗。 |
| 3 | 減衰・共振が確認できるか? | →パルスで減衰振動・共振を確認。 |
| 4 | 荷重がなくなっても振動するか? | →パルスで成功。周期では0か負の一定値をとる。 |
①パルスを加え、30%の減衰にして解析したところ、片持ち梁の時と同じく、 固有周期で減衰振動した。[固有振動数:約2800[Hz] 振動周期:約0.00036[sec]]
100[N]5.d-5[sec]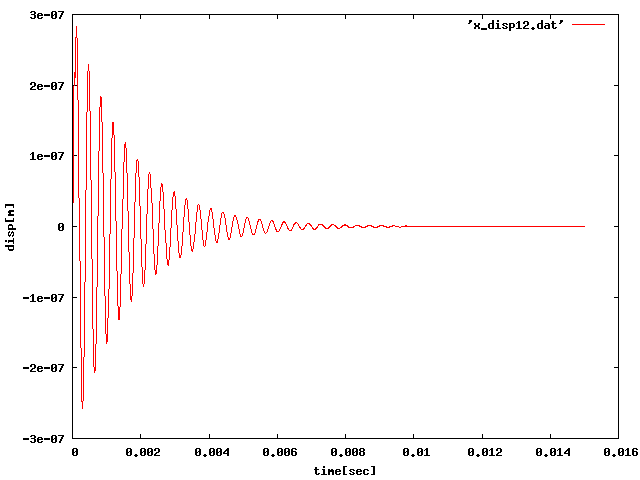 |
②周期荷重の正・負のみを含むように周期荷重を載荷した結果綺麗なsin波形となった。 しかし、荷重がなくなったあとは振動していないことがわかる。
| 100[N]1Hz0.5sec | 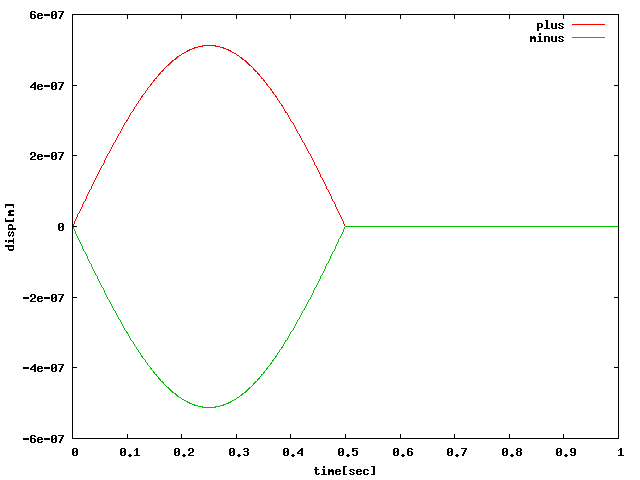 |
③負方向のみでパルスをかけてみたが、①と同じくただの減衰振動を示した。 周期荷重でも負に変位が大きく出たことから、蛇腹構造のバネ性能が、 モード解析において負の変位の増幅となって表れる可能性が高いのかもしれない。
| 10[N]5.d-5[sec] | 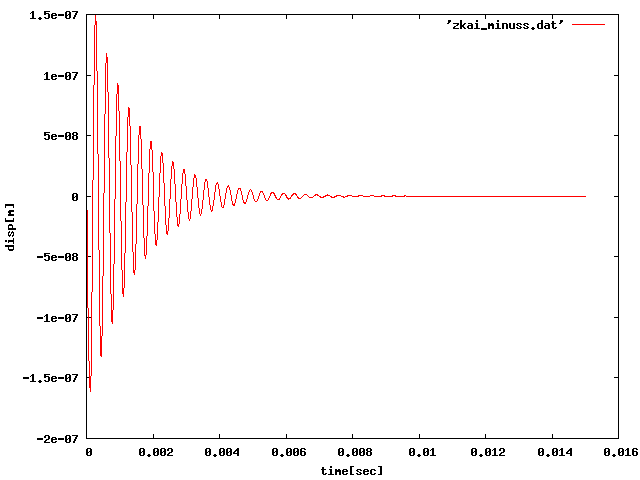 |
④条件が変わったので(載荷点のヤング率増大)、 もう一度周期荷重をかけて解析してみたが、前回の結果と同じだったため、 周期荷重での解析は正しくできない可能性が高い。
| 10[N]2Hz2sec | 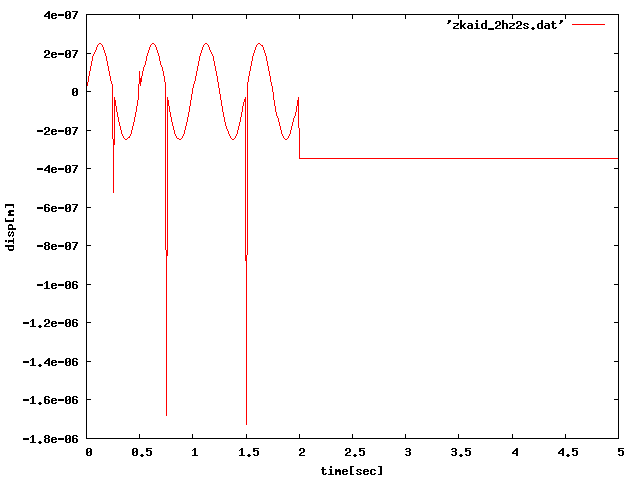 |
| パルスでの荷重定義を変えて解析してみる。 |
| plus_minus → ⑤ |
| onetempo → ⑥ |
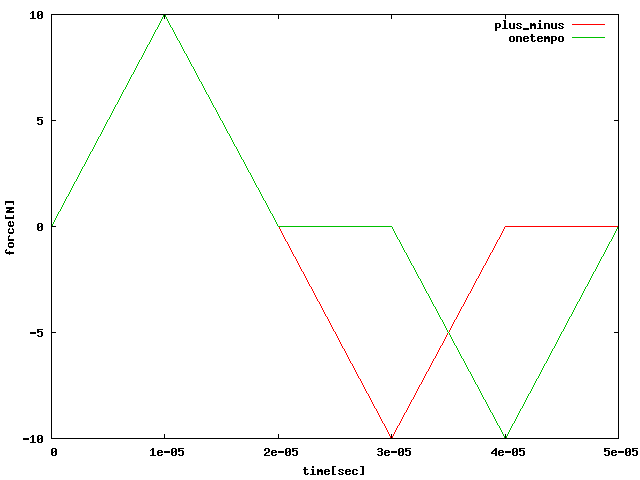 |
⑤パルスで正負を含むようにかけると負の範囲で減衰振動していた。 正負を含む荷重がゼロでつながっている場合に、 蛇腹構造のバネ性能の影響で負の変位が増大すると考えて⑦の方法で解析した。
| 10[N](正1→負1) | 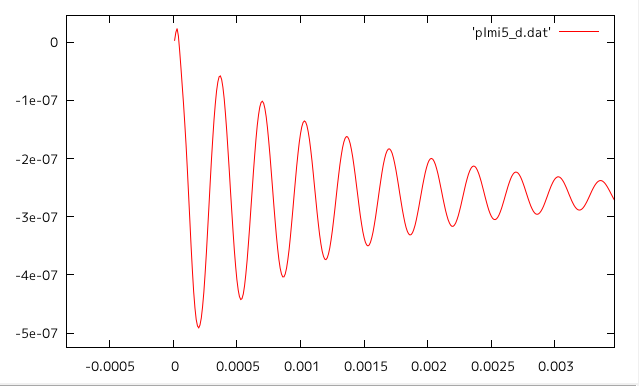 |
⑥正にかけた後、ワンテンポ遅れて負に同じ大きさと時間のパルスをかけて、 応答の違いを確認した。時間を開けた場合、減衰があってもなくても (↓のグラフは減衰あり)正負の変位が等しい減衰振動を示した。
| 時間ごとの荷重の定義 | |
| 10[N](正1→ゼロ→負1) | 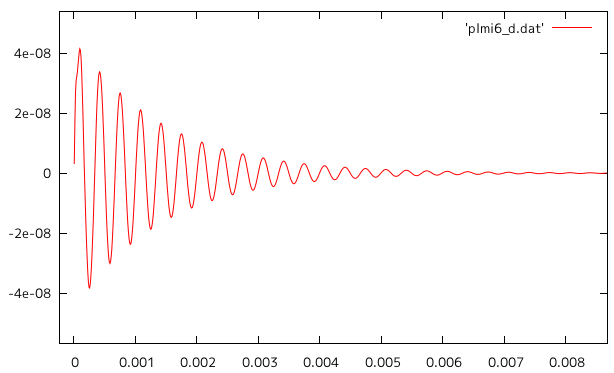 |
⑦固有振動数3000[Hz]に対して、共振する周期荷重をかけてみる。 今まで2[Hz]など地震に近い周期をかけていたが、あまり良い結果が得られなかったので、 共振するかを確認する。→共振してなおかつ荷重がなくなってからも減衰振動した。
| 10[N]3000[Hz]3.33d-3(100周期) | 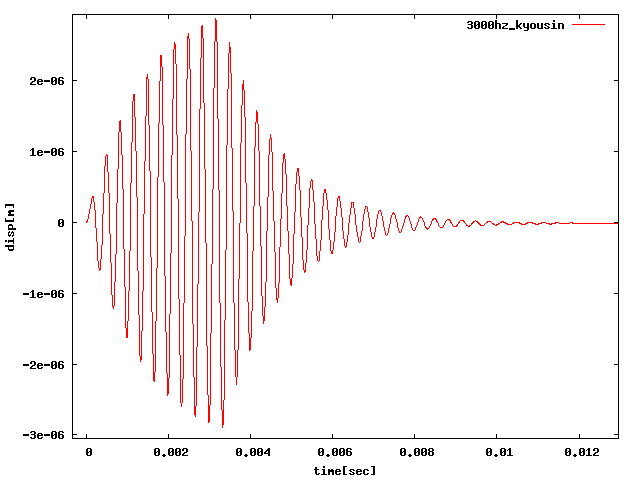 |
⑧振動数を変えて、どこまで固有振動するかを確認する。 100[Hz]を1周期掛けたところ、周期は荷重に依存し、 負に大きく変位することはなかったが、 荷重がなくなって以降は固有振動とはいえ負の範囲で減衰振動した。
| 10[N]100[Hz]0.01[sec] | 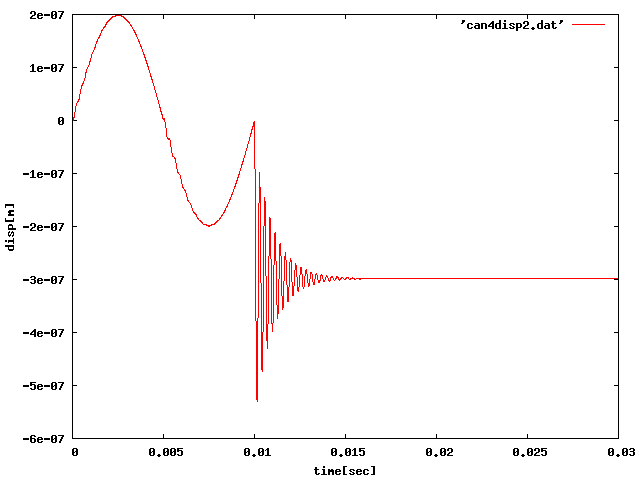 |
⑨ ⑤で正負を含むパルスをかけた場合に変位が負に傾くと示したが、 周方向・高さ方向分割を変更したモデルで解析した結果、 0を中心とした減衰振動となった。 しかし、別のモデルでは正の範囲で減衰振動したことからモデルや荷重によって変わる。
| 10[N]1.d-5 | 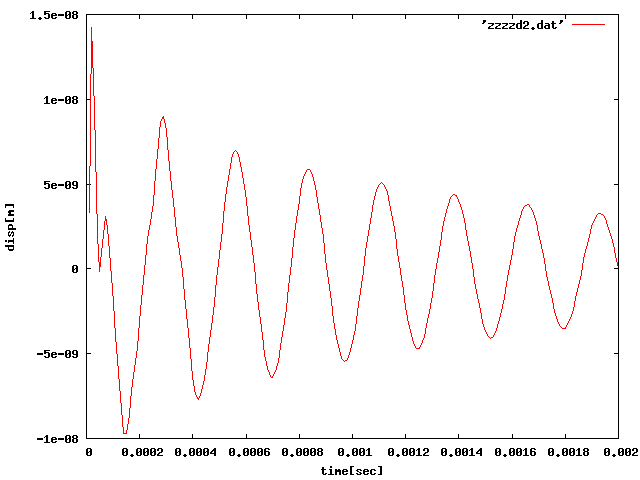 |
◆改善点:自由端の各節点に載荷すると自由端の節点ごとに変位が大きく異なったが、 自由端中心の一点に載荷すると(静的なたわみ解析結果と同じく)変位が ほぼ一定になった。→他のパラメータで解析しても同様になった。 シェル要素のモード解析では数点載荷が有効だと思われる。
片持ち梁の場合、周期荷重・パルス荷重に関係なく振動解析できていることがわかった。 振動も固有周期で出ているため、問題はないが、共振や減衰がソリッド要素に比べ、 はっきりと確認できていないためそれを確認したい。 以下のグラフで65Hzを0.4秒かけたものが最も大きく変位していることがわかるので、 共振していると言える。 減衰は蛇腹で確認できたので省略する。(周期=65[Hz],荷重は1[N])
| 1Hz4sec | 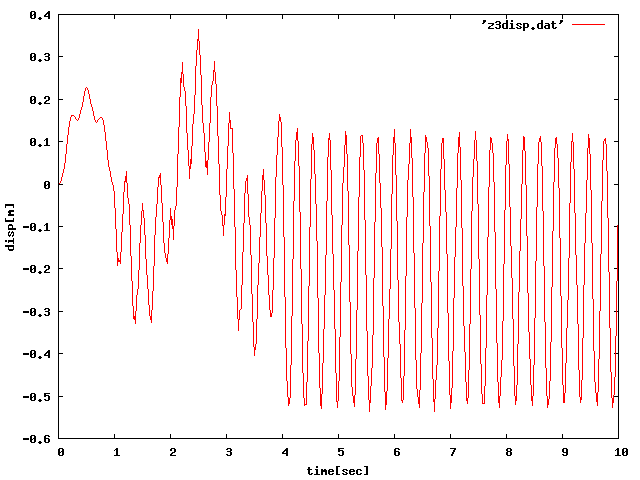 |
| 65Hz0.4sec | 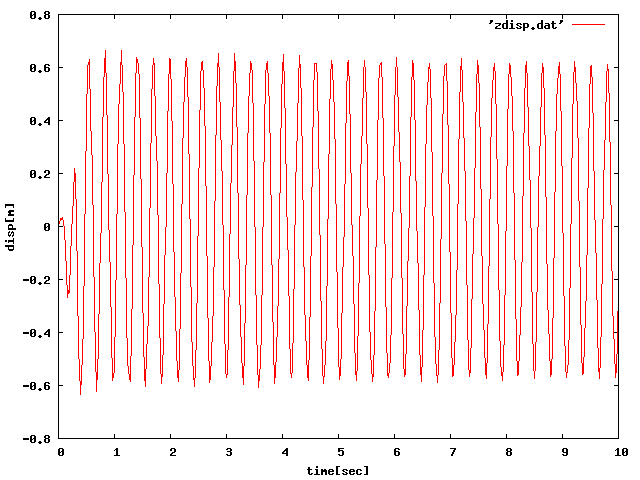 |
| 減衰なしパルス | 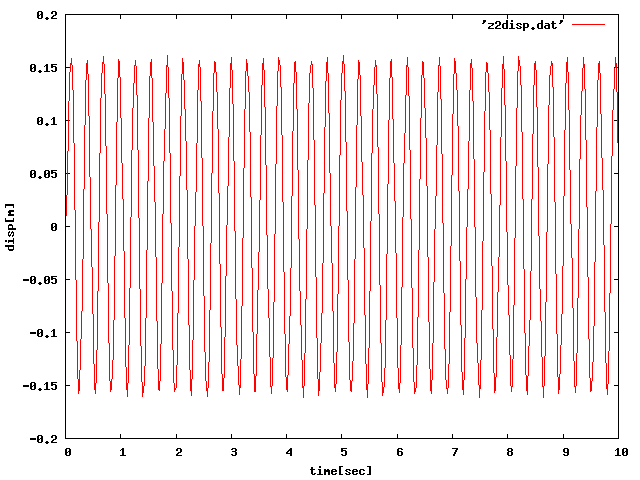 |
◆片持ち梁の自由端の節点を含む要素のヤング率を、 1000倍して分布荷重で載荷してみたが、変位は自由端の節点ごとに大きく異なったため、 蛇腹構造の載荷点に対しても同様の結果が出ることが予想される。 →蛇腹ではかなり有効となった。
片持ち梁(シェル要素)に対するモード解析結果を以下にまとめた。
| 載荷方法 | 荷重 | その他の変更点 | 自由端節点の変位 |
| 分布 | パルスor周期 | バラバラ | |
| 一点載荷 | パルスor周期 | 一定 | |
| 分布 | 周期(プラスのみ) | バラバラ | |
| 一点載荷 | 周期(プラスのみ) | 一定 | |
| 分布 | パルスor周期 | 自由端ヤング率を1000倍 | バラバラ |
| 一点載荷 | パルスor周期 | 自由端ヤング率を1000倍 | 一定 |
以上からシェル要素に対してモード解析を行った場合に、 載荷点(自由端)の変位が一定となるような結果を出すためには、 分布荷重ではなく、一点(片持ち梁の場合)載荷など載荷点を少なくする必要が あることがわかった。その理由として考えられるのは、 静的な解析におけるたわみの式とは異なり、時間ステップごとに固有振動モードの 重ね合わせで変位を求めているため、要素ごとに固有振動モードと荷重による変位を 計算しているからではないかと思われる。 (1要素に対して3点載荷されているため、要素ひとつずつが一次モードで変形している?) 一点載荷にした場合には、荷重が真ん中の一点のみにかかっているため、 モード解析をするために荷重がかかっていない要素も含めて、 自由端を1要素群とみなして解析されているため、 静解析と同じく変位が一定となって出るのではないか?
◆ステンレス材料で行い、厚さは 5 3 1 ミリで試す。 周方向分割数を4・6・8…(できれば円柱近似も行う)と変えてみて、鉛直・水平荷重に 対する応答を見てみる。荷重は変位が思ったより小さいので、1MNとした。
→①厚さ1 3 5ミリで4・6分割は解析できたが、8分割以上でエラーが生じて、 モード解析ができなくなった。固有振動数までは解析されているので、
→②高さの分割を10から16に変えたところで解析できた。 周方向分割数と折りたたみ段毎の高さの関係が原因かもしれない。 しかし、円柱近似にしようとすると別のエラーが表示された。 16分割に固定して周方向4・6・8分割に対して鉛直・水平の荷重をかけて解析してみる。
↑周方向による水平方向変位の違いをグラフにしたが、 周期荷重をかけているにも関わらず、荷重がなくなったところで振動せず、 一定の値を示すようになってしまった。 他の周期やステップでも試したが同様になったため改善する必要がある。
↑荷重をかけ続けてみたが、 sin波で振動するはずが途中で明らかに大きい値が生じていた。
| ① | 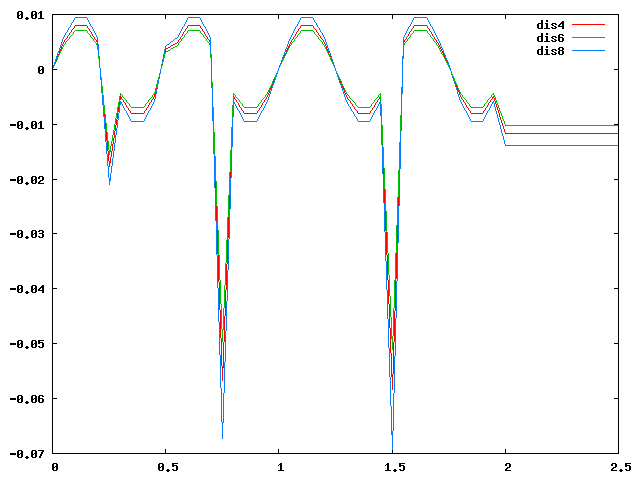 |
| ② | 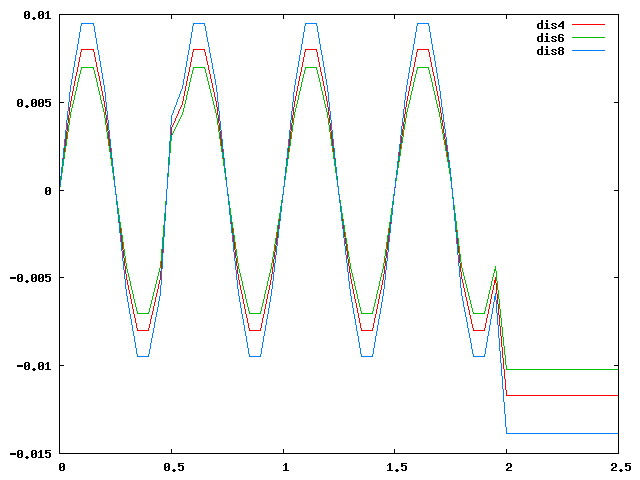 |
↑①のグラフは周期荷重を2Hzに変えて2秒かけてみたが、やはり0になるところで 変位が大きく出たので0に近い値に調整したところ②のようになった。
↑軸方向に鉛直荷重をかけてみたが、結局水平荷重と同様に減衰振動せず、 0になるところで変位が大きくなっていた。他の節点でも試したが、 同様の結果になったので境界条件などを詳しく見直してみる。 なお、円柱近似も試したが、結果は同じようなグラフとなった。
| [問題] | 0となるところで変位が非常に大きくでる(主にマイナス変位) |
| 減衰の設定を各構造ごとに変え20%に統一しているにも関わらず定常波になっている | |
| 荷重がなくなったところで変位が一定の負の値になってしまい、減衰振動しない | |
| 荷重の周期で値が出ているので振動していない可能性が高い? |
ステンレス材料について調べる
| SUS304 | 最も一般的に使用 | 197[GPa] | 比重=8 |
| SUS301 | 板バネ用(Cが多い) | 186[GPa] | 比重= |
| 特徴 |
| 耐食性・耐熱性が強い |
| 熱伝導性が低い(鉄の1/5ほど) |
| 通電性が非常に低い |
| 加工によって金属の組成が劣化し、弱い磁性を持つ |
| 塩素や酸の強い環境では腐食する |
| 溶接の熱影響を受けた部分で腐食割れを起こす可能性がある |
| 加工硬化が大きいが伸びが大きいため複雑な加工もできる |
| ほぼ100%リサイクル可能な材料であり、再資源化しやすい |
| 厚さ[mm] | n次mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] |
| 3 | 1 | 1646 | 2 | 1 | 1256 | 1 | 1 | 800 |
| 2 | 2818 | 2 | 2376 | 2 | 1711 | |||
| 3 | 2830 | 3 | 2376 | 3 | 1711 | |||
| 4 | 2830 | 4 | 2562 | 4 | 2290 | |||
| 5 | 3056 | 5 | 2741 | 5 | 2384 | |||
| 6 | 4033 | 6 | 3378 | 6 | 2385 | |||
| 7 | 4033 | 7 | 3378 | 7 | 2426 | |||
| 8 | 4869 | 8 | 3721 | 8 | 2426 | |||
| 9 | 5121 | 9 | 4292 | 9 | 3341 | |||
| 10 | 5373 | 10 | 4555 | 10 | 3543 |
▼周方向分割数が6の場合
| 厚さ[mm] | n次mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] |
| 3 | 1 | 1462 | 2 | 1 | 1116 | 1 | 1 | 734 |
| 2 | 2736 | 2 | 2312 | 2 | 1715 | |||
| 3 | 2736 | 3 | 2312 | 3 | 1715 | |||
| 4 | 3225 | 4 | 2962 | 4 | 2182 | |||
| 5 | 3225 | 5 | 2962 | 5 | 2499 | |||
| 6 | 3856 | 6 | 3255 | 6 | 2499 | |||
| 7 | 3856 | 7 | 3255 | 7 | 2682 | |||
| 8 | 4300 | 8 | 3294 | 8 | 2682 | |||
| 9 | 5451 | 9 | 4654 | 9 | 3460 | |||
| 10 | 5451 | 10 | 4654 | 10 | 3460 |
▼周方向分割数が4の場合
| 厚さ[mm] | n次mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] | 厚さ[mm] | mode | 振動数[Hz] |
| 3 | 1 | 1267 | 2 | 1 | 981 | 1 | 1 | 694 |
| 2 | 2585 | 2 | 2207 | 2 | 1746 | |||
| 3 | 2697 | 3 | 2297 | 3 | 1764 | |||
| 4 | 3596 | 4 | 2866 | 4 | 2035 | |||
| 5 | 3671 | 5 | 3194 | 5 | 2779 | |||
| 6 | 3674 | 6 | 3319 | 6 | 2793 | |||
| 7 | 3690 | 7 | 3342 | 7 | 2980 | |||
| 8 | 4283 | 8 | 4136 | 8 | 3224 | |||
| 9 | 4933 | 9 | 4217 | 9 | 3299 | |||
| 10 | 5047 | 10 | 4387 | 10 | 3399 |
※片持ち梁の時と同じく、厚さが薄く周方向分割数が少ないほど(変形しやすいほど)、 振動数は小さくなる傾向があることが確認できた。
●載荷点の鉛直方向以外の変位を固定した場合 一次モードの振動は決まって鉛直荷重をかけた時のようなバネ振動だった。 二次モード以降は4・6分割は同じだったが、8分割は異なる振動をした。 分割数によっては起こりやすい振動が変わることがわかった。
→載荷点の固定条件をなくしたら、一次モードの振動が曲げモードになった。 また、一次以降のモードではねじれモードも確認できた。 実際の支承は積層ゴム支承と同じく、鉛直、水平変位だけでなく、 回転変位も含まれるので、モード解析では、載荷点の固定条件をなくして 解析を行う方が良いと思われる。
→周方向8分割以上で厚さが5ミリのときに、一次モードの振動が曲げではなく、 開口部の変形(X・Y方向の変形)に変わってしまった。 [*MODAL DYNAMIC]で解析したいモードの指定ができないので(マニュアルになかった)、 8分割の5ミリは解析結果が別物になってしまう。 モード指定が本当にできないのか試す必要がある。
●振動現象における加速度、速度などの出力は可能か? 構造物にとって共振だけでなく、 振動そのものの速度や加速度も重要であるため出力できるか試してみたい。 → マニュアルを見たが、*NODE PRINT で変位を *print"U" で 出力するようにはできなかった。(速度だったら"V"のようなコマンドがない)
※過渡応答の変位がどれくらい正しいのか調べる必要があるので、 本などの1自由度系の例題をccxで解いて同じような結果が求められるか?
→株式会社アライドエンジニアリングの解析例を参考に解析して、 ほぼ同じグラフとなった。 (http://www.alde.co.jp/advc/examples/modaldynamicresponse/index.html)
縦軸:変位[m] 横軸:時間[sec]
4~5%ほど誤差が出たのは以下が原因だと思われる。
| ①例題は円形断面だが矩形で解析したこと |
| ②分割数に限界がある(細かすぎると時間がかかりすぎてフリーズした) |
これで過渡応答の解析の精度がソリッド要素において確かなことを確認。
| 減衰マトリックス | 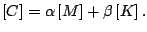 | M=質量マトリックス K=剛性マトリックス |
| 減衰定数 | 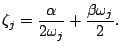 | $ω_{j}=固有角振動数$ |
ccxでは減衰の設定をマトリックスの係数でしていて、 臨界減衰(ζ=1)に対して何%の減衰としたいかは、一次モードの固有角振動数[rad/sec]を 計算してからでないと狙ってできないと思われる。 (おそらく*MODAL DYNAMIC では一次モードでの過渡応答が解析されるため、 一次モードに対して減衰の設定を変えれば任意の減衰を設定できるはずである。)
βの値を0.0002~2に渡って変えると↓のようなグラフになる。 βの設定値が大きいほど表の式より減衰定数ζが大きくなり、減衰が効いてくる。
| 0.002sec pulse10[N]f=65Hz | 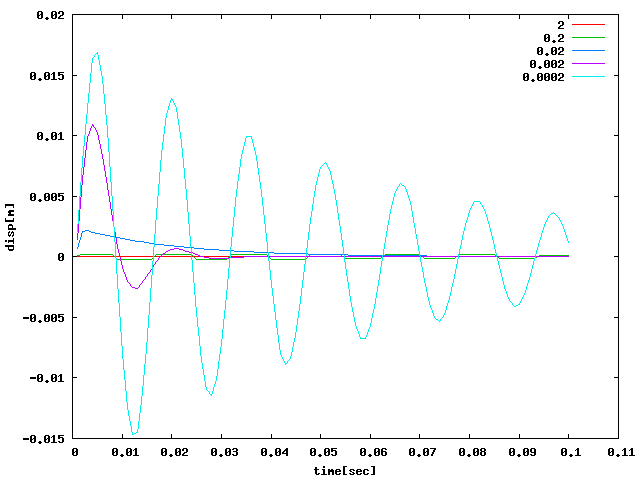 |
過減衰(ζ≧1)でない場合、ω=406[Hz]・α=0・β=2.0d-4 だと ζ=0.04 となり、 臨界減衰1に対して約25%減衰となるが、 必ずしも0.04×25=1だから25%減衰というように分かりやすい結果にはならないので、 一次固有振動数とグラフの値を確認して何%減衰か設定する必要がある。
一方、αの値を100・500・1000と変えると↓のようなグラフになり、 βと同様に設定値が大きいほど減衰が効く。
| 0.002sec pulse10[N]f=65Hz | 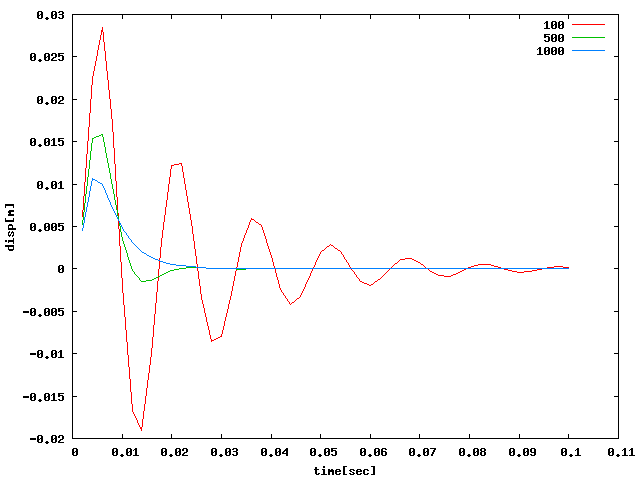 |
◆その他気づいたこと
[*MODAL DYNAMIC]でモード解析を行う場合、前の[*STEP]で[*FREQUENCY]が必要だが、 このとき求める固有値のモード数によって変位応答の結果が変わった。 これはモード解析が、 2次モード以降を振動モードの重ねあわせによって解析しているからで、 使用するモード数が多いほどより精度の高い解析ができると思われる。
平板要素でも試したが固有振動数の誤差が大きく、 時刻歴応答の固有周期に影響すると思われるのでソリッド要素で継続する。
訂正…値が+−に出たのは、減衰の設定によるものではなく、 解析する時間間隔を大きくしたからだった。 前回は細かすぎたため値が無限に大きくなっているように見えていた。[山の部分] 一次固有振動数からおおまかな時間間隔を予想して設定する必要がある。
●減衰の設定を変え、最終的な計算時間を伸ばし、間隔を細かくとったところ、 時間-変位グラフ[縦軸:m 横軸:sec]は綺麗なsin波形となり、 振幅は最終的に0になった(減衰振動)。 振動周期は一次固有振動数の逆数にほぼ等しくなった。
[1/65 = 0.015 sec] ※荷重はY(高さ)方向にかけている(幅:X=b 高さ:Y=h 軸長:Z= $\ell$)
| 10[N] | 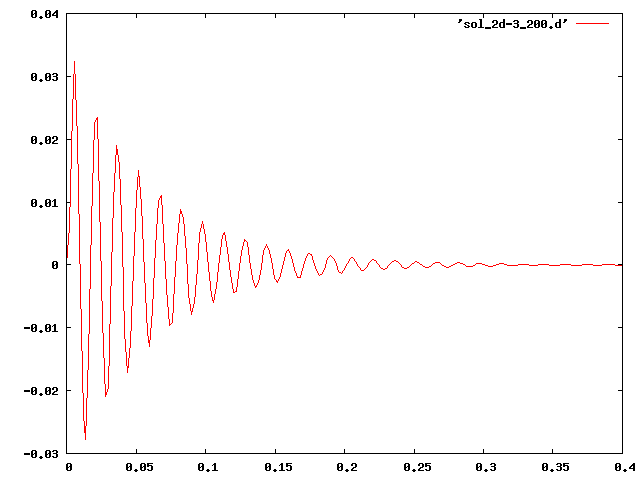 |
減衰定数は1を超えることはなく、超えた場合は振動しない。 減衰定数が1に近いほど効果は大きく、より振動変位が減小しやすくなる。(約25%減衰)
●共振現象を確認できるか試してみる。
※共振を確認するには、周期的な時間-荷重曲線[sin波]を別のファイルに作って読み込ませる必要がある。したがって、 固有振動の周期に近い時間-荷重曲線の値を表計算を利用してcsvファイルに書き込む。
①共振すると思われるデータを作成し、荷重の大きさを半分にして計算した結果、 減衰があるにも関わらず変位は前回結果よりも大幅に増大していた。
| 5[N] | 65[Hz] | 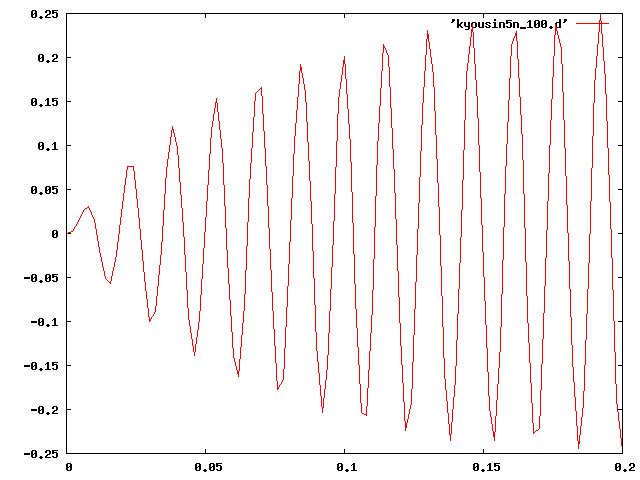 |
②共振しない時間-荷重曲線のデータも作成し、共振との違いを確認。 明らかに共振していない結果となった。
| 5[N] | 25[Hz] | 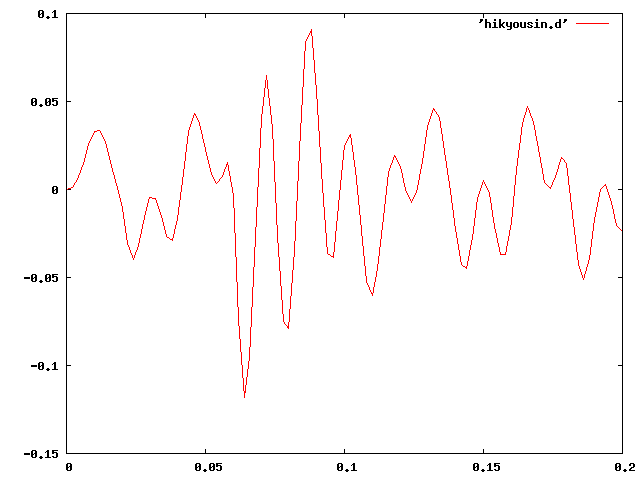 |
③二次モードの固有振動数に近い時間-荷重曲線ではどうなるか試してみる。 共振はしていないが、25[Hz]よりも振幅の変化が大きく出た。 固有振動が問題なのではなく、単純に振動数が増えたことにより、 振動が激しくなったと思われる。また、二次固有振動数で共振しなかったことから、 ccxによる過渡応答は一次モードで解析されることが分かる。
| 5[N] | 405[Hz] | 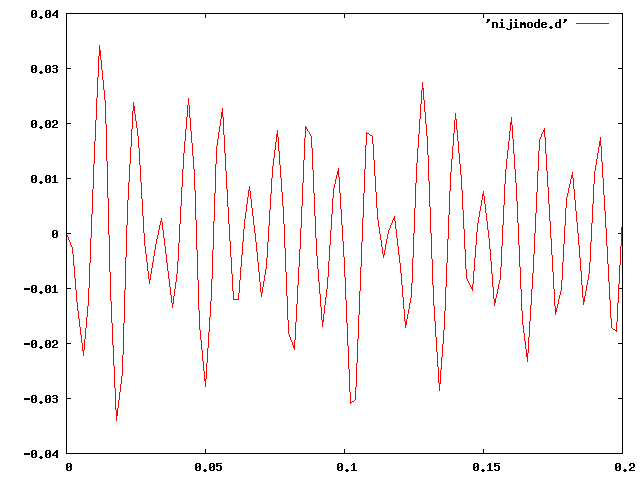 |
④定常波を表示できるか試してみる。 減衰設定をなくし、荷重をインパルス荷重にすることで確認できると思われる。 時間間隔のためかグラフが若干粗いが、振幅の極値はほとんど変わらず、 定常波の形になっている。
| 5[N] | 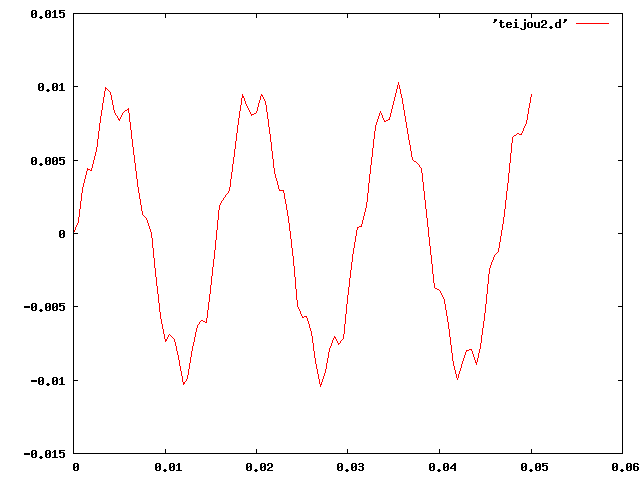 |
| 材料 | ヤング率[GPa] | ポアソン比 | 密度[$kg/m^3$] | 断面[m] | X:幅b | Y:高さh | Z:軸長 $\ell$ |
| アルミ | 70 | 0.33 | 2800 | 0.02 | 0.02 | 0.5 |
(ソリッド要素での要素分割数は X:4 Y:20 Z:150) ※ 正方形断面なのでX・Y方向曲げ固有振動数の区別は省略する。
●使用式
| 曲げ | 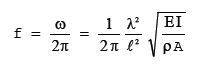 | [λ=1.875 4.694 7.855 …] | ||
| ねじれ | 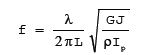 | 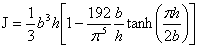 | $I_{P} = \frac{1}{12} (bh^3+b^3h)$ | [λ=$\frac{\pi}{2}$ $\frac{3\pi}{2}$ $\frac{5\pi}{2}$ …] |
| 伸縮 | 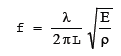 | [λ=$\frac{\pi}{2}$ $\frac{3\pi}{2}$ $\frac{5\pi}{2}$ …] |
※ねじれ式のGはせん断弾性係数でアルミの場合 26[$kN/mm^2$]
| 振動モード | 理論値[Hz] | 解析結果[Hz] | 誤差[%] |
| 一次曲げ | 64.61 | 65.16 | 0.85 |
| 一次ねじれ | 1383.81 | 1427.48 | 3.16 |
| 一次伸縮 | 2500.00 | 2504.34 | 0.17 |
| 二次曲げ | 404.93 | 405.34 | 0.10 |
| 二次ねじれ | 4151.44 | 4282.67 | 3.16 |
| 二次伸縮 | 7500.00 | 7511.33 | 0.15 |
| 三次曲げ | 1133.92 | 1121.83 | 1.07 |
| 三次ねじれ | 6919.07 | 7138.54 | 3.17 |
| 三次伸縮 | 12500.00 | 12513.27 | 0.11 |
ねじれ振動が最も変形が複雑となるので、 誤差は曲げ・伸縮に比べ大きく出たと考えられる。 また、正方形断面でない場合、 荷重の影響を大きく受ける弱軸方向曲げの誤差が増すことが予想される。
(cgxのデータセットでn次モードの固有振動数を指定し、アニメーションで確認)
※順番は構造によって異なり、振動数の低いモードから順に表示される。
モードが大きくなるにつれて誤差は大きくなる傾向が見られ、 要素数によってはモード数の大きい複雑な変形の解析結果は信用できない可能性が高い。
| モードNo | 振動モード | モードNo | 振動モード | モードNo | 振動モード |
| 1 | Y方向一次曲げ | 11 | Y方向五次曲げ | 21 | X方向八次曲げ |
| 2 | X方向一次曲げ | 12 | X方向五次曲げ | 22 | 四次ねじれ |
| 3 | Y方向二次曲げ | 13 | 二次ねじれ | 23 | Y方向九次曲げ |
| 4 | X方向二次曲げ | 14 | Y方向六次曲げ | 24 | X方向九次曲げ |
| 5 | Y方向三次曲げ | 15 | X方向六次曲げ | 25 | 三次伸縮 |
| 6 | X方向三次曲げ | 16 | Y方向七次曲げ | 26 | 五次ねじれ |
| 7 | 一次ねじれ | 17 | X方向七次曲げ | 以下略 | |
| 8 | Y方向四次曲げ | 18 | 三次ねじれ | ||
| 9 | X方向四次曲げ | 19 | 二次伸縮 | ||
| 10 | 一次伸縮 | 20 | Y方向八次曲げ |
ソリッド要素で3%になることを確認。結果の振動数はMODE NO 1,2 が、 ほぼ同じ値であったため、曲げモードは1次につき2つずつ出力されると思われる。 よって、2次はMODE NO 3,4 、3次はMODE NO 5,6 と比較すると、 それぞれ誤差は1%未満となった。→2つずつ出力されたのは、 Y方向とX方向の曲げ固有振動数を表示しているためで、 正方形断面だったからほぼ同じ値だった。
| 材料:アルミ | ヤング率:70GPa | ポアソン比:0.33 | 荷重:10N | |||
| 断面(m) | 幅(x):0.04 | 板厚(y):0.004 | 長さ(z):1.00 | 要素分割 | X方向:20 | Z方向:20 |
| 弱軸(Y方向)に載荷 : 理論値 = 223.21(mm) | 解析値 = 196.05(mm) | 誤差 12.17% | ||||
| 強軸(X方向)に載荷 : 理論値 = 2.2321(mm) | 解析値 = 2.2270(mm) | 誤差 0.23% |
| Z(再計算:X2Y6Z475) | 理論値 7.2464(mm) | 再計算収束値 7.1544(mm) |
プログラム先頭のdimensionの上限を増すことでより要素分割数を増やし、 理論値に近づくことを確認 X6 Y10 Z700 のとき収束値 7.2067(mm) Z方向の要素数が値に大きく影響しているが、 X2 Y2 Z1000 よりも X2 Y6 Z475 の方が理論値に近くなった。 また、X2 Y10 Z300 よりも X2 Y6 Z475 の方が理論値に近かったことから、 Y方向とZ方向の要素数のバランスが重要だと思われる。
| 日付 | 曜日 | 開始〜終了 | 作業時間(h) | 立合 | 作業内容 | |
| 4/25 | 月曜 | 16:00~18:00 | 2.00 | 江村 | vi編集 | |
| 4/28 | 木曜 | 14:30~18:00 | 2.50 | 後藤 | vi編集 | |
| 5/9 | 月曜 | 16:00~18:00 | 2.00 | 柴田 | vi編集(最大最小) | |
| 5/12 | 木曜 | 14:30~17:00 | 2.00 | 後藤 | vi編集 (最大最小) | |
| 5/13 | 金曜 | 13:00~17:00 | 3.00 | 江村 | vi編集(最大最小) | |
| 5/16 | 月曜 | 16:00~19:00 | 3.00 | 後藤 | ccx片持ち梁要素分析 | |
| 5/17 | 火曜 | 13:00~17:00 | 3.00 | 後藤 | ccx片持ち梁要素分析 | |
| 5/18 | 水曜 | 13:00~16:00 | 2.00 | 柴田 | ccx片持ち梁要素分析 | |
| 5/19 | 木曜 | 13:00~16:00 | 2.00 | 江村 | ccx片持ち梁要素分析 | |
| 5/23 | 月曜 | 16:00~19:00 | 3.00 | 江村 | htmlファイル作成・ccx片持ち梁要素分析 | |
| 5/24 | 火曜 | 13:00~16:00 | 2.00 | 柴田 | ccx片持ち梁要素分析 | |
| 5/30 | 月曜 | 16:00~18:00 | 2.00 | 後藤 | ccx片持ち梁要素分析・Tex練習 | |
| 6/2 | 木曜 | 14:30~17:30 | 3.00 | 後藤 | 折りたたみプログラム導入・Tex | |
| 6/6 | 月曜 | 16:00~18:00 | 2.00 | 後藤 | シェル要素分析 | |
| 6/7 | 火曜 | 14:00~16:00 | 2.00 | 江村 | シェル要素分析 | |
| 6/9 | 木曜 | 14:00~19:00 | 4.00 | 後藤 | シェル要素分析 | |
| 6/10 | 金曜 | 14:00~19:00 | 4.00 | 後藤 | シェル要素分析 | |
| 6/11 | 土曜 | 13:00~18:00 | 4.00 | 後藤 | シェル要素分析 | |
| 6/13 | 月曜 | 16:00~18:00 | 2.00 | 後藤 | 固有振動 | |
| 6/14 | 火曜 | 10:00~14:00 | 3.00 | 後藤 | 固有振動 | |
| 6/16 | 木曜 | 17:00~19:00 | 2.00 | 後藤 | 固有振動 | |
| 6/17 | 金曜 | 14:00~18:00 | 4.00 | 後藤 | 固有振動 | |
| 6/20 | 月曜 | 16:00~18:00 | 2.00 | 後藤 | モード解析 | |
| 6/23 | 木曜 | 9:00~17:00 | 6.00 | 後藤 | モード解析 | |
| 6/24 | 金曜 | 12:30~18:00 | 5.00 | 柴田 | モード解析 | |
| 6/27 | 月曜 | 17:00~19:00 | 2.00 | 柴田 | モード解析 | |
| 6/28 | 火曜 | 15:00~17:00 | 2.00 | 後藤 | モード解析 | |
| 6/29 | 水曜 | 13:00~20:00 | 6.00 | 後藤 | モード解析 | |
| 6/30 | 木曜 | 14:00~16:00 | 2.00 | 後藤 | モード解析 | |
| 7/2 | 土曜 | 15:00~17:00 | 2.00 | 後藤 | モード解析 | |
| 7/4 | 月曜 | 16:00~18:00 | 2.00 | 後藤 | モード解析 | |
| 7/5 | 火曜 | 10:00~17:00 | 5.00 | 柴田 | モード解析 | |
| 7/6 | 水曜 | 14:00~16:00 | 2.00 | 柴田 | モード解析 | |
| 7/7 | 木曜 | 15:00~17:00 | 2.00 | 後藤 | モード解析 | |
| 7/8 | 金曜 | 9:00~17:00 | 7.00 | 後藤 | モード解析 | |
| 7/11 | 月曜 | 16:30~18:30 | 2.00 | 後藤 | モード解析 | |
| 7/12 | 火曜 | 13:00~16:00 | 3.00 | 後藤 | モード解析 | |
| 7/14 | 木曜 | 14:00~17:00 | 3.00 | 後藤 | モード解析 | |
| 7/16 | 土曜 | 13:00~17:00 | 4.00 | 柴田 | モード解析 | |
| 7/22 | 金曜 | 15:00~18:00 | 3.00 | 柴田 | モード解析 | |
| 7/23 | 土曜 | 14:00~16:00 | 2.00 | 柴田 | モード解析 | |
| 7/24 | 日曜 | 7:00~8:00 | 1.00 | 柴田 | モード解析 | |
| 7/25 | 月曜 | 7:00~8:00 | 1.00 | 柴田 | モード解析 | |
| 7/26 | 火曜 | 12:00~17:00 | 5.00 | 後藤 | モード解析(精度確認) | |
| 7/27 | 水曜 | 13:00~15:00 | 2.00 | 後藤 | モード解析(精度確認) | |
| 7/30 | 土曜 | 12:00~17:00 | 5.00 | 柴田 | モード解析(精度確認) | |
| 8/3 | 水曜 | 11:00~18:00 | 6.00 | 後藤 | モード解析(蛇腹の固有値解析)+振り子作成 | |
| 8/4 | 木曜 | 12:00~17:00 | 5.00 | 後藤 | モード解析(蛇腹の固有値解析)+振り子作成 | |
| 8/5 | 金曜 | 10:30~20:30 | 8.00 | 柴田 | モード解析(蛇腹の固有値解析)+OC準備 | |
| 8/6 | 土曜 | 14:00~18:00 | 4.00 | 柴田 | モード解析(蛇腹の固有値解析)+OC準備 | |
| 8/22 | 月曜 | 13:00~16:00 | 3.00 | 後藤 | モード解析(精度確認再開) | |
| 8/23 | 火曜 | 14:30~17:00 | 2.50 | 後藤 | モード解析(精度確認) | |
| 8/24 | 水曜 | 13:00~19:00 | 4.50 | 江村 | モード解析(精度確認) | |
| 8/25 | 木曜 | 9:00~12:00 | 3.00 | 柴田 | モード解析(精度確認) | |
| 8/26 | 金曜 | 14:00~18:00 | 4.00 | 柴田 | モード解析(精度確認) | |
| 8/28 | 日曜 | 15:00~19:00 | 4.00 | 柴田 | モード解析(精度確認) | |
| 8/29 | 月曜 | 15:00~17:00 | 2.00 | 後藤 | モード解析(精度確認) | |
| 8/30 | 火曜 | 15:00~18:00 | 3.00 | 柴田 | モード解析(精度確認終了) | |
| 8/31 | 水曜 | 13:00~18:00 | 4.00 | 柴田 | モード解析(蛇腹の過渡応答開始 試算) | |
| 9/1 | 木曜 | 13:00~14:30 18:00~20:30 | 4.00 | 柴田 | モード解析(4 6分割 鉛直 厚さ3種) | |
| 9/4 | 日曜 | 13:00~17:00 | 4.00 | 柴田 | モード解析(8分割解析 鉛直・水平荷重 厚さ3種) | |
| 9/24 | 土曜 | 17:00~20:00 | 3.00 | 柴田 | モード解析(周方向比較 水平荷重) | |
| 9/25 | 日曜 | 14:00~16:00 | 2.00 | 柴田 | モード解析(周方向比較 水平荷重) | |
| 9/26 | 月曜 | 12:00~15:00 | 3.00 | 江村 | モード解析(周方向比較 水平荷重) | |
| 9/27 | 火曜 | 14:00~20:00 | 4.00 | 江村 | モード解析(周方向比較 水平・鉛直荷重) | |
| 9/28 | 水曜 | 14:00~15:00 | 1.00 | 後藤 | tex関係 | |
| 9/29 | 木曜 | 13:00~18:00 | 5.00 | 後藤 | tex関係+pdf作成 | |
| 9/30 | 金曜 | 15:00~20:00 | 5.00 | 後藤 | tex関係+pdf作成 | |
| 10/1 | 土曜 | 12:00~14:30 | 2.50 | 柴田 | tex関係+pdf作成 | |
| 10/3 | 月曜 | 14:00~17:00 | 3.00 | 後藤 | tex関係+pdf作成 解析確認 | |
| 10/5 | 水曜 | 10:30~21:00 | 6.00 | 後藤 | シェルに対するモード解析(片持ち) | |
| 10/7 | 金曜 | 16:00~20:00 | 4.00 | 後藤 | シェルに対するモード解析(蛇腹)+tex | |
| 10/8 | 土曜 | 16:00~22:00 | 6.00 | 後藤 | シェルに対するモード解析(片持ち)+tex | |
| 10/9 | 日曜 | 20:00~24:00 | 4.00 | 柴田 | シェルに対するモード解析(蛇腹)+tex | |
| 10/10 | 月曜 | 10:00~13:00 | 3.00 | 柴田 | シェルに対するモード解析(蛇腹)+tex | |
| 10/13 | 木曜 | 15:00~17:00 | 2.00 | 柴田 | シェルに対するモード解析(蛇腹) | |
| 10/14 | 金曜 | 15:00~20:00 | 5.00 | 江村 | シェルに対するモード解析(蛇腹) | |
| 10/16 | 日曜 | 13:00~19:00 | 5.00 | 柴田 | シェルに対するモード解析(蛇腹) | |
| 10/18 | 火曜 | 13:00~20:00 | 5.00 | 江村 | シェルに対するモード解析(蛇腹) | |
| 10/19 | 水曜 | 13:00~17:00 | 4.00 | 後藤 | モード解析+OC準備 | |
| 10/20 | 木曜 | 16:00~22:00 | 4.00 | 江村 | シェルに対するモード解析(蛇腹) | |
| 10/25 | 火曜 | 14:30~22:00 | 5.00 | 江村 | シェルに対するモード解析(蛇腹) | |
| 10/27 | 木曜 | 17:00~22:00 | 4.00 | 柴田 | シェルに対するモード解析(片持ち梁) | |
| 10/28 | 金曜 | 16:00~19:00 | 3.00 | 江村 | シェルに対するモード解析(蛇腹) | |
| 11/5 | 土曜 | 17:00~19:00 | 2.00 | 柴田 | シェルに対するモード解析(片持ち梁+蛇腹) | |
| 11/6 | 日曜 | 15:00~20:00 | 5.00 | 柴田 | シェルに対するモード解析(片持ち梁) | |
| 11/7 | 月曜 | 17:00~24:00 | 6.00 | 柴田 | DLOADによるシェル要素モード解析 | |
| 11/8 | 火曜 | 17:00~23:00 | 5.00 | 柴田 | DLOADによるシェル要素モード解析 | |
| 11/9 | 水曜 | 14:00~19:00 | 5.00 | 江村 | DLOADによるシェル要素のたわみ解析 | |
| 11/12 | 土曜 | 10:30~20:00 | 7.00 | 柴田 | DLOADによるシェル要素のたわみ解析 | |
| 11/13 | 日曜 | 17:30~21:00 | 3.00 | 柴田 | DLOADによるシェル要素のたわみ解析 | |
| 11/14 | 月曜 | 15:00~20:00 | 5.00 | 後藤 | DLOADによるソリッド要素のたわみ解析 | |
| 11/15 | 火曜 | 14:00~20:30 | 6.00 | 後藤 | DLOADによるソリッド要素のたわみ解析 | |
| 11/16 | 水曜 | 16:00~22:00 | 4.50 | 後藤 | 薄板を載せた蛇腹折りモード解析+ccx2.3との比較 | |
| 11/18 | 金曜 | 14:00~21:00 | 5.00 | 後藤 | 薄板を載せた蛇腹折りモード解析 | |
| 11/21 | 月曜 | 14:30~21:30 | 5.00 | 後藤 | 薄板を載せた蛇腹折りモード解析 | |
| 11/22 | 火曜 | 11:20~12:20 | 1.00 | 後藤 | 薄板を載せた蛇腹折りモード解析 | |
| 11/22 | 火曜 | 19:00~22:00 | 3.00 | 後藤 | 薄板を載せた蛇腹折りモード解析+ccx2.3との比較 | |
| 11/25 | 金曜 | 14:30~22:30 | 4.50 | 後藤 | ABAQUSが使えるか?+DLOAD確認 | |
| 11/27 | 日曜 | 15:00~21:00 | 6.00 | 柴田 | ABAQUS(試)+DLOAD確認(済) | |
| 11/28 | 月曜 | 16:30~21:30 | 5.00 | 江村 | 解析手法による比較(蛇腹) | |
| 11/29 | 火曜 | 15:00~21:00 | 6.00 | 江村 | 厚さ・荷重方向による比較+BEAM要素での拘束 | |
| 11/30 | 水曜 | 12:00~14:00 | 2.00 | 後藤 | 時間ステップでの比較 | |
| 12/2 | 金曜 | 14:30~22:30 | 6.50 | 柴田 | 高さ分割数比較・BEAM拘束・その他新たに解析 | |
| 12/4 | 日曜 | 13:00~19:00 | 6.00 | 柴田 | 直接法・複数荷重の同時入力・減衰設定の再確認 | |
| 12/5 | 月曜 | 18:00~25:00 | 6.00 | 柴田 | 初期高さ比較・ソリッド載荷 | |
| 12/6 | 火曜 | 18:30~24:00 | 4.00 | 柴田 | 減衰振動比較・ソリッド載荷 | |
| 12/7 | 水曜 | 8:00~12:00 | 4.00 | 後藤 | ソリッド載荷・複数荷重の入力・塑性入力(試) | |
| 12/8 | 木曜 | 16:30~24:00 | 6.50 | 柴田 | 荷重の変更によりグラフは変わるか? | |
| 12/9 | 金曜 | 14:00~24:00 | 7.00 | 柴田 | 切れ目の追加・固有値グラフ・固有振動数の低減 | |
| 12/10 | 土曜 | 0:00~2.00 | 2.00 | 柴田 | 初期高さによる固有値比較 | |
| 12/10 | 土曜 | 15:00~22:00 | 6.00 | 柴田 | 固有値比較・固有振動数下げて周期荷重応答 | |
| 12/13 | 火曜 | 14:00~24:00 | 5.00 | 柴田 | 固有振動数下げてモード解析・固有値比較 | |
| 12/14 | 水曜 | 13:00~22:00 | 7.00 | 後藤 | 中間発表スライド作成+モード解析(比較) | |
| 12/15 | 木曜 | 13:00~24:00 | 7.00 | 柴田 | 中間発表スライド作成+モード解析(比較) | |
| 12/16 | 金曜 | 13:30~20:30 | 6.00 | 柴田 | 中間発表スライド作成+発表練習 | |
| 12/17 | 土曜 | 15:00~17:00 | 2.00 | 柴田 | 中間発表スライド修正 | |
| 12/18 | 日曜 | 13:30~18:30 | 5.00 | 柴田 | 中間発表準備・発表練習 | |
| 12/22 | 木曜 | 6:00~16:30 | 8.50 | 後藤 | 弾塑性モデルの作成・回転変位のグラフ化・設計反力 | |
| 12/23 | 金曜 | 15:00~24:00 | 8.00 | 後藤 | 初期高さと固有値比較・弾塑性解析 | |
| 12/25 | 日曜 | 15:00~19:00 | 4.00 | 後藤 | 周波数による応答比較・塑性の設定・回転荷重 | |
| 12/27 | 火曜 | 13:30~18:30 | 5.00 | 後藤 | 周波数による応答比較・塑性の設定・回転荷重 | |
| 1/6 | 金曜 | 7:00~17:00 | 8.00 | 後藤 | 周波数による応答比較・周波数応答解析 | |
| 1/10 | 火曜 | 15:00~21:00 | 4.00 | 後藤 | 周波数応答解析・長短周期振動について | |
| 1/11 | 水曜 | 10:30~18:00 | 6.00 | 後藤 | 周波数応答解析・色々メモ | |
| 1/16 | 月曜 | 14:00~22:00 | 7.00 | 後藤 | 周波数応答解析 | |
| 1/17 | 火曜 | 14:00~19:00 | 4.00 | 後藤 | スライド改良・tex | |
| 1/18 | 水曜 | 13:00~22:00 | 8.00 | 後藤 | 支部概要作成(グラフ以外) | |
| 1/19 | 木曜 | 18:00~24:00 | 6.00 | 後藤 | 支部概要作成(グラフ→完了) | |
| 1/20 | 金曜 | 10:00~14:00 | 4.00 | 後藤 | 支部概要添削 | |
| 1/21 | 土曜 | 20:00~24:00 | 4.00 | 後藤 | 支部概要改良 | |
| 1/22 | 日曜 | 9:00~12:00 | 3.00 | 後藤 | 卒論スライド作成 | |
| 1/23 | 月曜 | 15:00~19:00 | 3.00 | 後藤 | 卒論スライド作成 | |
| 1/24 | 火曜 | 19:00~22:00 | 3.00 | 後藤 | 支部概要訂正 | |
| 1/25 | 水曜 | 12:00~15:00 | 3.00 | 後藤 | 支部概要送信 スライドver1完成 | |
| 1/26 | 木曜 | 18:00~24:00 | 6.00 | 江村 | スライド修正 tex | |
| 1/27 | 金曜 | 17:00~24.00 | 5.00 | 江村 | スライド tex | |
| 1/28 | 土曜 | 21:00~24.00 | 3.00 | 後藤 | スライド tex | |
| 1/29 | 日曜 | 5:00~10.00 | 4.00 | 後藤 | スライド tex | |
| 1/30 | 月曜 | 15:00~21.00 | 6.00 | 後藤 | スライド tex | |
| 1/31 | 火曜 | 9:00~24:00 | 8.00 | 後藤 | 発表練習+スライド修正 | |
| 2/1 | 水曜 | 15:00~24:00 | 6.00 | 後藤 | スライド修正 | |
| 2/2 | 木曜 | 5:00~12:00 | 6.00 | 後藤 | スライド修正 減衰定数の評価(試) | |
| 2/3 | 金曜 | 3:00~22:00 | 10.00 | 後藤 | スライド修正(完)・減衰定数の評価(試) | |
| 2/4 | 土曜 | 17:00~24:00 | 7.00 | 柴田 | スライド補足・ソリッドとシェルは一致するか? | |
| 2/5 | 日曜 | 6:00~19:00 | 10.00 | 柴田 | スライド補足・シェル要素の振動解析精度再確認 | |
| 2/6 | 月曜 | 15:00~17:00 | 2.00 | 後藤 | スライド補足 | |
| 合計 | 613.5(h) |
自分の研究では、振動解析を行ったわけだが…正直な話、大した結果は出なかった。 (序盤に自分が馬鹿なことが原因で、振動解析の方法や意味を理解する段階で、 時間をかけすぎてしまった。より早い段階でモード解析の精度と蛇腹折りモデルでの モード解析が正しくできていれば、 他の解析も試せたと思うので少しだけ後悔している。)
結局、剛性と密度に依存した結果となり、地震応答解析の論文に見るような 複雑な応答スペクトル波形や加速度応答・速度応答を解析できなかった。 地盤の状態や地震のような複雑な揺れを設定して 解析できれば面白い結果が出たのだろうか?(Calculixで可能だったのか?)
もしくは、梁要素で橋梁のモデルを作り、 支承部分に蛇腹折りを複数使用したモデルを作る必要があるのだろうか? そして、複数バネの挙動を調べる必要があると思われる。 (なによりも実物の性能を調べることが先決だが…)