2023 春課題座屈解析の履歴(No.13) - PukiWiki

[ トップ ] [ 新規 | 一覧 | 検索 | 最終更新 | ヘルプ | ログイン ]

進捗状況
- 2月23日
- 2月28日
- 3月1日
- 3月2日
解析結果

進捗状況†

2月23日†

座屈解析の方法はわかったが、座屈荷重の求め方がわからない状態にある。

座屈解析の進捗としては片持ち梁の鋼材と木材の解析を行なった後、片持ちばりの両端固定と両端ピンと両端固定のときのスパン長を2倍にして行った。それから等方性から異方性に変えて解析を行った。　

2月28日†

座屈荷重の求め方を教えてもらった。片持ちばりの木材鋼材について解析し、またメッシュサイズも変えて行った。

3月1日†

各々で解析を行いデータを解析結果として記していく。

3月2日†

片持梁の解析結果を増やした。両端固定した座屈解析がうまく行かない。

解析結果†

2月28日†

10×5×100　木材　等方性　載荷荷重2000N　理論値　強軸方向　616.85N　弱軸方向　154.212N メッシュサイズ１†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
１	181.25	644.124
２	1604.212	5419.96
３	4303.46
４	8047.18

10×5×100　鋼材　等方性　載荷荷重50000N　理論値　強軸方向　21075.9N　弱軸方向　5268.9N メッシュサイズ１†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
１	5985.8	21720.8
２	53009.5	183459
３	142513

10×5×100　木材　等方性　載荷荷重2000N　理論値　強軸方向　616.85N　弱軸方向　154.212N メッシュサイズ５†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
１	877.664	1118.266
２	6915.62	8945.6

3月1日†

座屈荷重理論式（オイラー座屈）†

\( P=(\frac{π}{k\ell})^{2}EI \)

片持ちの場合:k=2

両端固定の場合:k=0.5

両端ピン固定の場合:k=1

固定＋ピン固定の場合:k=0.7

10×5×100　木材　異方性　片持梁　載荷荷重2000N　理論値　強軸方向　616.85N　弱軸方向　154.212N 高井†

座屈モード	0.5弱軸方向｛N｝	0.5強軸方向｛N｝	0.6弱軸方向｛N｝	0.6強軸方向｛N｝	0.7弱軸方向｛N｝	0.7強軸方向｛N｝	0.8弱軸方向｛N｝	0.8強軸方向｛N｝	0.9弱軸方向｛N｝	0.9強軸方向｛N｝	1.0弱軸方向｛N｝	1.0強軸方向｛N｝
１	155.48	596.512	155.521	596.554	160.0956	600.118	163.99	602.798	164.96	603.05	164.36	602.99

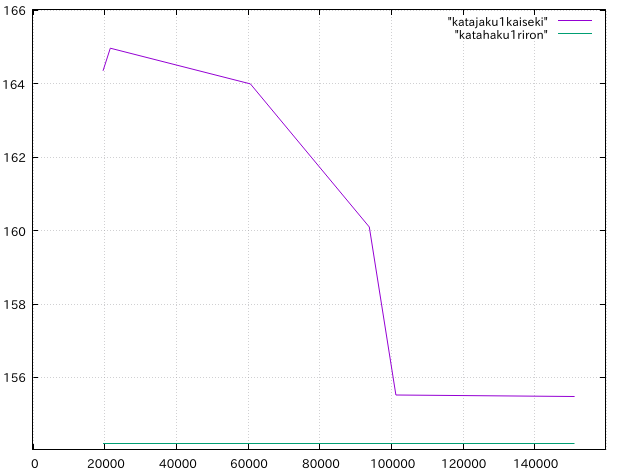
理論値：弱軸方向　154.212N

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
0.5	151096	155.48	0.82
0.6	101211	155.521	0.85
0.7	93797	160.0956	3.82
0.8	60625	163.99	6.34
0.9	21520	164.96	6.97
1.0	19543	164.36	6.58

・弱軸方向の要素数と座屈荷重の関係

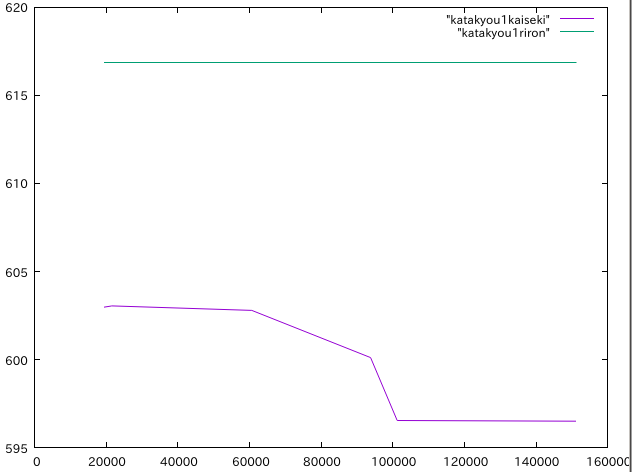
理論値：強軸方向　616.85N

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
0.5	151096	596.512	-3.30
0.6	101211	596.554	-3.29
0.7	93797	600.118	-2.71
0.8	60625	602.798	-2.28
0.9	21520	603.05	-2.24
1.0	19543	602.99	-2.25

・強軸方向の要素数と座屈荷重の関係

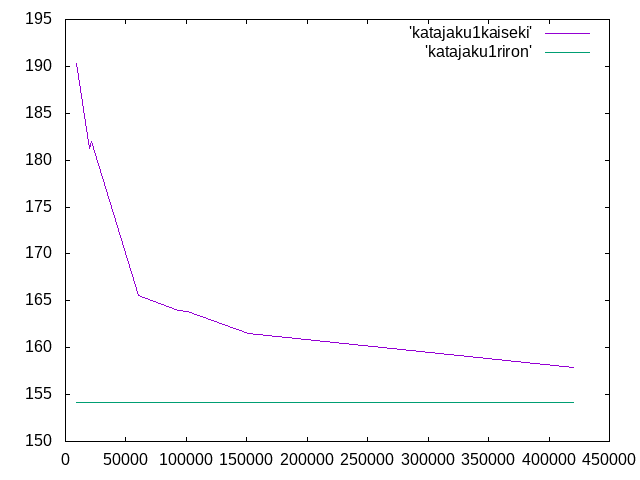
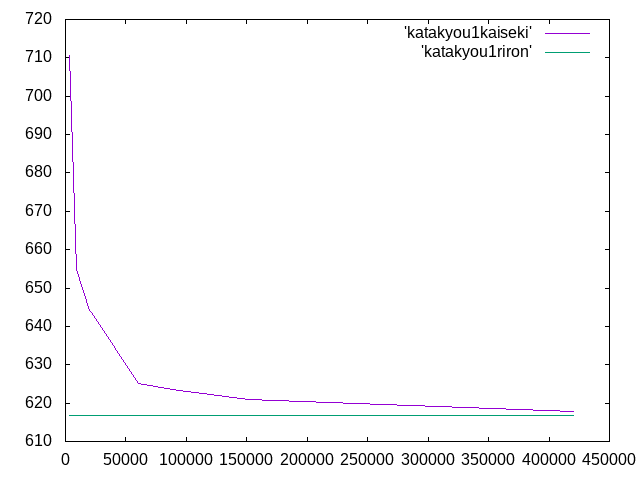
10×5×100　木材　等方性　片持梁　１次モード　載荷荷重3000N　理論値　弱軸方向　154.212N　強軸方向　616.85N 岡田†

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}	強軸方向｛N｝	相対誤差{%}
0.4	420533	157.91	2.4	617.95	0.2
0.5	151096	161.48	4.7	621.02	0.7
0.6	101211	163.82	6.2	623.02	1.0
0.7	93797	163.97	6.3	623.28	1.0
0.8	60625	165.61	7.4	625.10	1.3
0.9	21520	181.96	18.0	643.60	4.3
1.0	19543	181.25	17.5	644.12	4.4
1.5	9252	190.28	23.4	654.74	6.1
2.0	2928	280.38	81.8	710.74	15.2

・弱軸方向の要素数と座屈荷重の関係

・強軸方向の要素数と座屈荷重の関係

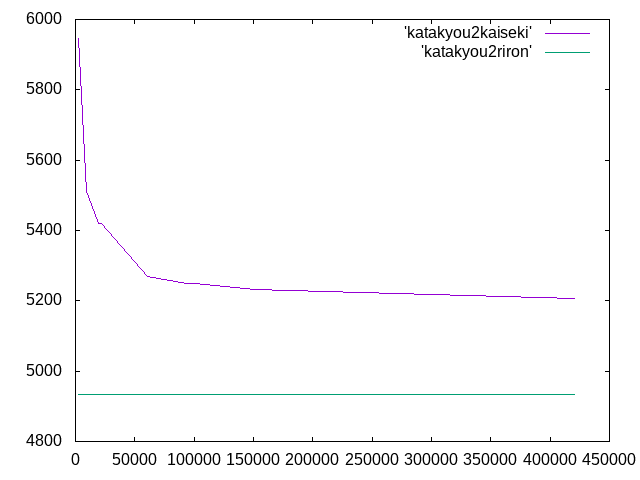
10×5×100　木材　等方性　片持梁　2次モード　載荷荷重3000N　理論値　弱軸方向　1233.70N　強軸方向　4934.8N 岡田†

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}	強軸方向｛N｝	相対誤差{%}
0.4	420533	1398.723	13.3	5206.86	5.5
0.5	151096	1429.68	15.9	5232.48	6.0
0.6	101211	1450.239	17.6	5248.89	6.4
0.7	93797	1451.622	17.7	5250.48	6.4
0.8	60625	1467.732	19.0	5268	6.8
0.9	21520	1611.57	31.0	5419.1	9.8
1.0	19543	1604.212	30.0	5419.96	9.8
1.5	9252	1682.265	36.3	5509.95	11.7
2.0	2928	2445.381	98.2	5946.57	20.5

・弱軸方向の要素数と座屈荷重の関係

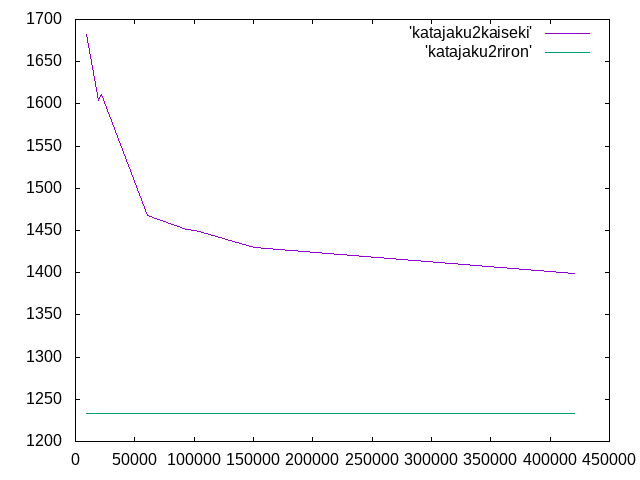
・強軸方向の要素数と座屈荷重の関係

4月11日†

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ0.5　要素数　137993　以下山口†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
１	636.225	3448.74
２	2477.343	7801.74
３	5305.62
４	7374.27

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ0.6　要素数　94482†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
1	644.835	3566.22
2	2512.446	9017.46
3	5401.56
4	8724.81

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ0.7　要素数　87760†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
1	644.919	3602.73
2	2512.779	9195.3
3	5411.82
4	9014.04

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ0.8　要素数　50763†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
1	658.809	3682.35
2	2563.875	9502.29
3	5532.36
4	9255.69

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ0.9　要素数　46015†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
1	660.048	3680.37
2	2567.793	9513.84
3	5542.68
4	9284.61

10×5×100　木材　ピン固定　載荷荷重3000N　理論値　強軸方向　5035.512N　弱軸方向　1258.878N メッシュサイズ1　要素数　19700†

座屈モード	弱軸方向｛N｝	強軸方向｛N｝
1	709.32	3806.64
2	2757.744	9820.95
3	5939.25
4	9903.24

ピン固定1次モード

理論値：弱軸方向　616.85N

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
0.5	137993	636.225	3.14
0.6	94482	644.835	4.54
0.7	87760	644.919	4.55
0.8	50763	658.809	6.80
0.9	46015	660.048	7.00
1.0	19700	709.32	14.99

理論値：強軸方向　2467.40N

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
0.5	137993	3448.74	39.77
0.6	94482	3566.22	44.53
0.7	87760	3602.73	46.01
0.8	50763	3682.35	49.24
0.9	46015	3680.37	49.16
1.0	19700	3806.64	54.28

ピン固定2次モード

理論値：弱軸方向　2467.4 N

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
0.5	137993	2477.343	0.40
0.6	94482	2512.446	1.83
0.7	87760	2512.779	1.84
0.8	50763	2563.875	3.90
0.9	46015	2567.793	4.07
1.0	19700	2757.744	11.77

理論値：強軸方向　9869.6 N

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
0.5	137993	7801.74	-20.95
0.6	94482	9017.46	-8.63
0.7	87760	9195.3	-6.83
0.8	50763	9502.29	-3.72
0.9	46015	9513.84	-3.60
1.0	19700	9820.95	-0.49

4月14日†

10×1×100　木材　等方性　片持梁　1次モード　２次要素　載荷荷重 200N　岡田†

理論値：弱軸方向　1.2337N

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
0.5	28919	1.2492	1.26
0.6	20577	1.249314	1.27
0.7	14585	1.250232	1.34
0.8	11210	1.2455	0.96
0.9	8877	1.250754	1.38
1.0	7183	1.251184	1.42

理論値：強軸方向　123.37N

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
0.5	28919	122.6826	-0.56
0.6	20577	122.6896	-0.55
0.7	14585	122.7086	-0.54
0.8	11210	122.717	-0.53
0.9	8877	122.7314	-0.52
1.0	7183	122.7422	-0.51

4月17日追加分

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
1.5	2891	1.251184	1.52
3.0	692	1.262064	2.30
4.0	377	1.270912	3.02
5.5	244	1.285016	4.16
6.0	198	1.287154	4.33

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
1.5	2891	122.794	-0.47
3.0	692	123.1098	-0.21
4.0	377	123.3916	0.02
5.5	244	123.6984	0.27
6.0	198	123.7798	0.33

4月17日†

10×1×100　木材　等方性　片持梁　1次モード　 1次要素　載荷荷重 400N　高井†

理論値：弱軸方向　1.2337N

メッシュサイズ	要素数	弱軸方向｛N｝	相対誤差{%}
1.5	2891	6.87116	456.98
2.0	1813	6.082	392.98

理論値：強軸方向　123.37N

メッシュサイズ	要素数	強軸方向｛N｝	相対誤差{%}
1.5	2891	130.0216	5.39
2.0	1813	131.6712	6.72