秋山の修論日誌の履歴(No.106)

修論
Marc_mentant　地震応答解析
重力荷重・斜張橋モデル_ケーブル・分割(2mにつき1要素)
- 断面2次モーメントを任意で与える
- 地震応答解析（水平方向）
斜張橋モデル_modal300{ケーブル・分割(2mにつき1要素)}
斜張橋モデル_model300(ケーブル・1要素)
斜張橋モデル_model600
- 断面照査
- 地震解析
簡易モデル
Marc_mentant　連鎖崩壊
斜張橋モデル
marcメモ
- 弾性域のひずみ
- 終了番号
salome_meca
参考資料
メモ
東北支部
土木学会全国大会
日記

修論†

テーマ：ケーブル腐食を考慮した斜張橋の他用な外力が作用した際の数値解析的検討

ケーブル破断の要因の一つに地震が考えられる
→地震荷重でケーブルが破断しない，ケーブルのひずみが増幅しない（model300）
→ケーブルの揺れを再現し，重力やサグのような方向，モデル化の検討

Marc_mentant　地震応答解析†

例題により確立した方法で地震解析を進めていく。
入力変位は神戸にて観測された兵庫県南部地震の加速度を変位に変えたものを使用する。

加速度では地震解析がいかなかった.
（初期位置からX方向(地震波入力方向)プラスの位置に移動し，収束する）
→各ポイント間（データポイントの時間差：0.02秒）でそれぞれ積分してほしいが，前のデータを含めて積分しているのではないか？
→Marc上で加速度を積分すると（速度にすると）右肩上がりになる

入力変位

減衰定数は0.005，Newmarcβ法を用いて動的解析を行った

↑

重力荷重・斜張橋モデル_ケーブル・分割(2mにつき1要素)†

死荷重の載荷をやめ，重力荷重をモデル橋全体に載荷させた

今までのケーブル1要素の時の変形図

ケーブルを2mにつき1要素になるように分割したもの，変形図

C1の材料特性で重力荷重

↑

断面2次モーメントを任意で与える†

下にとんでもないたわみがでる理由:曲げ剛性~ ケーブルは曲げ剛性を無視し，伸び剛性と張力の影響でたわむ
梁要素でケーブルを表現しているので，たわみは梁のたわみ方（伸び剛性と曲げ剛性の影響）になっている
→→→曲げ剛性の影響を無くしたい

C1のみ，とりあえずIxxとIyyを100に

全ケーブルIxxとIyyを100に→エラー2004
全ケーブルIxxとIyyを50に→エラー2004
全ケーブルIxxとIyyを10に→エラー2004
全ケーブルIxxとIyyを1に→エラー2004
全ケーブルIxxとIyyを0.5に→エラー2004
全ケーブルIxxとIyyを0.1に→成功（下図）

スケールファクター10倍

断面2次モーメント0.1でも，もとの円形の丸鋼の断面2次モーメントの10000倍あるから十分か

↑

地震応答解析（水平方向）†

解析結果

↑

斜張橋モデル_modal300{ケーブル・分割(2mにつき1要素)}†

ケーブルを揺らす，ケーブルのフレキシブルな振動特性の反映

↑

線形解析†

主桁鉛直方向変位

https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/akiyama/disp_hikaku.png

線形解析により設計荷重を載荷．以前までと変化はない

↑

モード解析_フィルター無し†

解析結果

1 3.0365e-08

2 3.0372e-08

3 3.6659e-08

4 3.6659e-08

5 4.3269e-08

6 4.3329e-08

7 5.1289e-08

8 5.1300e-08

9 5.2535e-08

10 5.2550e-08

1次モード
2次モード
3次モード
4次モード
5次モード
6次モード
7次モード
8次モード
9次モード
10次モード

↑

理論値と比較†

弦の固有振動数の理論値
Fn=n/2l*(S/ρ)^(1/2)
l:減の長さ　n:腹の数　S:張力　ρ:線密度

計算結果

斜張橋のケーブル張力が反映されていない
→Prが-100℃のとき「3.0365e-08」
Prが-500℃のとき「3.0365e-08」

↑

地震応答解析(ケーブル2mにつき1要素)†

スケールファクター5倍

主桁スパン中央・水平方向変位

主桁スパン中央・上フランジ左端の応力

主桁には変化，影響はない

C1応力（桁端部の節点と中央部の節点で比較）

C1ひずみ（桁端部の節点と中央部の節点で比較）

ケーブル応力，ひずみは端部と中央部で一致した

C1の応力（1要素と分割時の比較）

C1のひずみ（1要素と分割時の比較）

C1の応力とひずみはケーブルが1要素時と分割時で一致した

C1の水平方向変位(t=258.63s)

C1のひずみ(t=258.63s)

1要素時と分割時で水平方向変位が異なるが，ひずみは一致した

C1の水平方向変位

ケーブルは揺れている

C1のひずみ履歴（ケーブル長で比較）

↑

モード解析†

1	0.499711
2	0.499907
3	0.499916
4	0.499942
5	0.51945
6	0.519703
7	0.519711
8	0.519723
9	0.525998
10	0.526032

1次モード
2次モード
3次モード
4次モード
5次モード
6次モード
7次モード
8次モード
9次モード
10次モード

↑

斜張橋モデル_model300(ケーブル・1要素)†

角田さん（角田さんの修論日誌）が作成した斜張橋モデルに地震波を入力する．

解析モデル，解析概要

↓斜張橋モデル

↓境界条件

地震波を橋軸直角方向に入力
○モデル諸元
主桁...SM400材（降伏点：235MPa）
主塔...SM490材（降伏点：315MPa）
ケーブル...ST1570(平行線ケーブルPWS)であり，第１降伏点：1160MPa，第２降伏点：1576MPa

↓主桁，主塔断面

↑

断面照査†

橋軸方向単位長さあたりの死荷重(D)は，鋼桁重量(69.7kN/m)，地覆・高欄(24.5kN/m)，アスファルト舗装(28.34kN/m)である．
また，端支点の不反力を抑制するため，側径間にカウンターウエイト(CW，80kN/m）を載荷した．
死荷重作用時に主桁および主塔の曲げモーメントが平滑化かつ最小になるようにケーブルプレストレス(Pr)を導入した．
活荷重(L)は道路橋示方書のB活荷重を準用することとし，スパン中央部に主催化荷重を載荷することとした．
すなわち，集中荷重p1(10kN/m2)を長さ10mおよび幅員5.5mに作用させる．ただしその他の部分は5.0kN/m2とする．
さらに分布荷重p2(3.0kN/m2)を幅員5.5mに作用させる．ただし，その他の部分は1.5kN/m2とする．なお，集中荷重はスパン中央に，等分布荷重は全径間に載荷した．
これらの荷重を載荷し，照査値が1.0を下回るように断面を設定した．

常時設計荷重

照査結果
a)主桁照査結果

b)主塔照査結果

c)ケーブル照査結果

d)照査結果まとめ

↑

断面積減少†

○各ケーブルの断面減少率とそのときの直径

cable	健全時	減少率30%	減少率60%
C1	0.150	0.1255	0.0949
C2 C3	0.127	0.1063	0.0803
C4 C5	0.122	0.1021	0.0772
C6 C7	0.085	0.0711	0.0538
C8-C10	0.121	0.1012	0.0765
C11-C13	0.124	0.1037	0.0784

健全時をcase1，減少率30%をcase2，減少率60%をcase3と述べる

↑

橋軸直角方向†

主桁中央の変位

主桁上フランジ上縁の応力（最大値をとった時刻）

主塔の曲げモーメント(最大値をとった時刻)

C1のケーブル張力

layer比較

〇主桁の右端のlayerを比較した．振幅は変わらない

○得られた知見

水平方向変位は各ケース等しくなる→変位に関してケーブル腐食の影響は少ない
case3では主桁スパン中央部付近で上フランジ上縁は降伏応力に達していた
主塔基部は腐食の進行度に比例し曲げモーメントは大きくなる
地震荷重は250sから載荷するが，ケーブル張力は地震荷重によって変化すること（スパイクする）はなかった
ケーブル腐食はケーブル張力ではなく，主塔および主桁に大きな影響を与える

↑

橋軸鉛直方向†

鉛直方向変位

主桁上フランジ上縁応力（最大値をとった時刻）

主塔曲げモーメント（最大値をとった時刻）

C1張力

〇得られた知見

鉛直方向ではケーブル張力がスパイクした
各応答値は腐食の進行度と比例している
case3は主桁スパン中央付近で降伏応力に至った

↑

破断ひずみ（応力ひずみ関係）の減少†

破断ひずみを減少させることでケーブル腐食を再現した．

減少率30%（破断ひずみ：0.012，第2降伏応力：1099MPa）をcase4
減少率60%（破断ひずみ：0.008，第2降伏応力：628MPa）をcase5と述べる

↑

橋軸水平方向†

主桁スパン中央部の水平方向変位

主桁上フランジ上縁の応力（最大値をとった時刻）

主塔の曲げモーメント（最大値をとった時刻）

C1のケーブル張力

〇得られた知見

case1とcase4は値が一致する
ケーブル腐食は主桁および主塔に大きな影響を与える

↑

橋軸鉛直方向†

主桁スパン中央の鉛直方向変位

主桁上フランジ上縁の応力（最大値をとった時刻）

主塔の曲げモーメント（最大値をとった時刻）

C1張力

〇得られた知見

case1とcase4の各応答値は概ね一致した
case5はスパン中央付近で降伏応力に到達しなかった

↑

異なる腐食の再現方法の比較†

断面積の減少，破断ひずみの低下（応力ひずみ関係の減少）の2種類で，減少率が等しいもの同士を比較する

σA=Fより，σが減少率した場合とAが減少率した場合は等しくなるはず．

↑

水平方向，30%†

主桁スパン中央の水平方向変位

C1張力

主桁上フランジ上縁応力

主塔基部の曲げモーメント

・断面積の減少によって再現した場合の方が応答値は大きくなる．

↑

水平方向，60%†

主桁スパン中央の水平方向変位

C1張力

主桁上フランジ上縁応力

主塔基部の曲げモーメント

↑

鉛直方向，30%†

主桁スパン中央の水平方向変位

C1張力

主桁上フランジ上縁応力

主塔基部の曲げモーメント

↑

鉛直方向，60%†

主桁スパン中央の水平方向変位

C1張力

主桁上フランジ上縁応力

主塔基部の曲げモーメント

断面積の減少によって再現した場合の方が応答値（ケーブル張力は応力にすると断面積減少の方)が大きな値になる~

Prをケーブルに温度（-200℃）を与えることで再現している．~
断面積減少，応力ひずみ関係の減少ともに熱膨張による応力は等しいが，力にすると断面積が異なるため変化する．~
そのため，断面積減少時はPrが小さくなり，応力ひずみ関係により腐食を再現した場合と比較して，構造的に弱くなっていると考える~

↑

減衰†

〇maecの減衰の与え方

角部材ごとに減衰を与える
レーリー減衰では，質量マトリクス乗数，剛性マトリクス乗数を与える
減衰乗数だけを与える

marcの和訳の乗数とは？→計算された値，すなわち質量比例減衰α，合成比例減衰β，減衰定数hと考える~
α=2hω,β=2h/ω,h:減衰定数（h=c/2mω）,c:減衰係数

現在，減衰は減衰乗数を与えている．与えている値は0.0032（一般的に吊り橋に用いられる減衰値）
→子の与え方が正しいか検討の必要有

One of the most frequent causes of problems analyzing elastomers is the incompressible material behavior. Lagrangian
multipliers (pressure variables) are used to apply the incompressibility constraint. The result is that the volume is kept
constant in a generalized sense, over an element.
Both the total, as well as updated Lagrange formulations, are implemented with appropriate constraint ratios for lowerand
higher-order elements in 2-D and 3-D. For many practical analysis, the LBB (Ladyszhenskaya-Babuska-Brezzi)
condition does not have to be satisfied in the strictest sense; for example, four node quadrilateral based on Herrmann
principle.
For elements that satisfy the LBB condition, error estimates of the following form can be established
(4-41)
where and are the orders of displacements and pressure interpolations, respectively. If , the rate
of convergence is said to be optimal, and elements satisfying the LBB condition would not lock.
The large strain elasticity formulation may also be used with conventional plane stress, membrane, and shell elements when
using the total Lagrance method. Because of the plane stress conditions, the incompressibility constraint can be satisfied

現在の減衰（画面）
例題ファイル（減衰2%）

1 5.771+0 6.929-5 0

0 0 0 0

自分のモデル（減衰3%）

1 0 0 3.00-2

0 0 0 0

a編86p，非圧縮性材料

without the use of Lagrange multipliers.

レーリー減衰について

https://www.forum8.co.jp/topic/up132-support-topics-ES.htm~

https://www.simscale.com/knowledge-base/rayleigh-damping-coefficients/ より

In this case one needs two damping ratios and two natural frequencies to create a pair of equations and solve for α and β. The model gives some flexibility on where to place the natural 
frequencies, but in general, frequencies too far away from the ones used in the computation will be amplified.

In the particular case of using equal damping ratios for the two frequencies, it is important to note that the damping ratio will not be constant inside the range defined by the sample 
points, but the inner frequencies will be attenuated. That is, the inner frequencies will have a lower damping ratio.

和訳

この場合，2 つの減衰比と 2 つの固有振動数で一組の方程式を作成し，α とβを解く必要がある．このモデルでは，固有振動数をどこに配置するかについてある程度の柔軟性があるが，
一般に，計算で使用した振動数から離れすぎた振動数は増幅される．

2つの周波数に等しい減衰比を使用する特殊なケースでは、減衰比はサンプルポイントで定義された範囲内で一定ではなく、内側の周波数が減衰することに注意する必要があります。
つまり、内側の周波数はより低いダンピング比を持つことになる。

↑

減衰の与え方†

marc_mentantでの減衰の与え方（レーリー減衰）
質量マトリクス乗数α，剛性マトリクス乗数βを計算し，数値を入力する．

〇手順
1.モード解析を行う
2.αとβを計算する
3.計算した値を入力する

αとβの計算式，画面

sin波を１周期だけ与えたときの動的応答解析結果

上記の結果より減衰定数を計算

減衰定数が2%になることを確認

↑

減衰定数の選定†

一般的な構造物の減衰定数を以下に示す
吊り橋：0.002～0.08
道路橋：0.02～0.05(コンクリート橋を含む)
鋼製タワー：0.002～0.03
鉄骨建物：0.003～0.04

このことを考慮し，減衰が小さいほど地震時のリスクが上がることから，減衰は比較的小さい0.005を適用した．

↑

地震メモ†

非線形地震応答解析による橋梁の耐震補強法

↑

斜張橋モデル_model600†

↑

断面照査†

橋軸方向単位長さあたりの死荷重(D)は，鋼桁重量(85.5kN/m)，地覆・高欄(24.5kN/m)，アスファルト舗装(28.34kN/m)である．
また，端支点の不反力を抑制するため，側径間にカウンターウエイト(CW，60kN/m）を載荷した．死荷重作用時に主桁および主塔の曲げモーメントが平滑化かつ最小になるようにケーブルプレストレス(Pr)を導入した．活荷重(L)は道路橋示方書のB活荷重を準用することとし，スパン中央部に主催化荷重を載荷することとした．すなわち，集中荷重p1(10kN/m2)を長さ10mおよび幅員5.5mに作用させる．ただしその他の部分は5.0kN/m2とする．さらに分布荷重p2(3.0kN/m2)を幅員5.5mに作用させる．ただし，その他の部分は1.5kN/m2とする．なお，集中荷重はスパン中央に，等分布荷重は全径間に載荷した．これらの荷重を載荷し，照査値が1.0を下回るように断面を設定した

主桁照査結果

主塔照査結果

ケーブル照査結果

全体の照査結果

↑

地震解析†

直角方向→error 1001
どうやればエラーがなおるかがわからない

マニュアルでは接触解析中のエラーなら片面接触をオンに．~
それ以外はタイイング（結合）のエラーか，システムのエラー~

↑

簡易モデル†

○モデル諸元

↑簡易モデル

・複雑な斜張橋モデルに地震をかける前に、Marcに慣れること、非線形解析などまだ行ったことがない解析を行うため、片持ち梁をケーブルで吊ったモデル(簡易モデル)に地震をかける
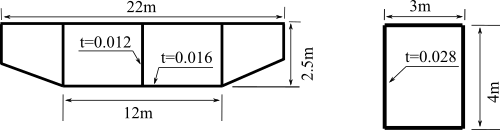
桁部分はSM400材と仮定しており、ヤング率は200GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。
断面が10mm×10mmの長さ1000mmの部材。ケーブル部分は平行線ケーブルPWSと仮定しており、ヤング率は195GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。線膨張係数は1.25e-5である。
ケーブルの直径は5mmであり、桁の固定端から高さ1000mmの位置に固定している。回転自由である。
節点温度を-200℃とし、ケーブルプレストレスを導入する。
SM400、PWSそれぞれに応力-ひずみ関係（構成則）を適用し、非線形解析とした。
固定端に兵庫県南部地震の変位を入力した。

○解析結果

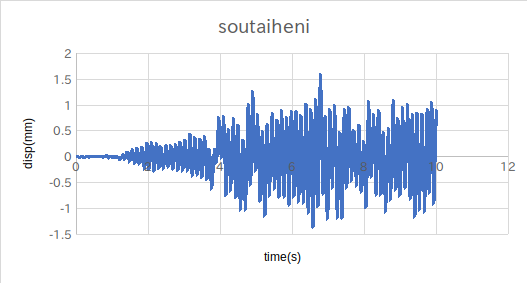
↑先端部分の相対変位
挙動として妥当であると言える。

しかし桁の基部が降伏点の235MPaに達していた。(圧縮引張ともに)
→正方形断面の1辺の長さを100mmに変更

○解析結果

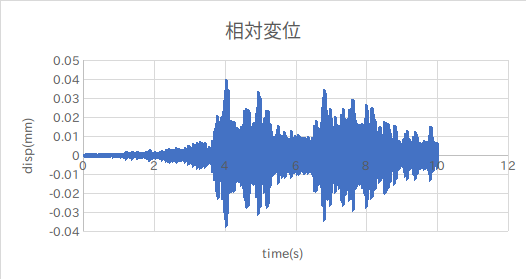
↑先端部分の相対変位
挙動として妥当であると言える。

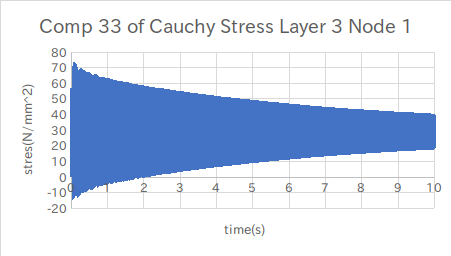
↑Z方向?の応力(引張)

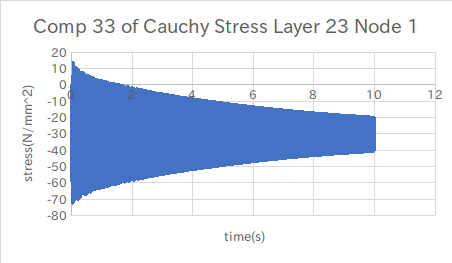
↑Z方向?の応力(圧縮)

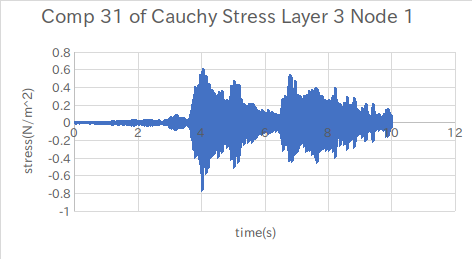
↑ZX方向?の応力(引張)

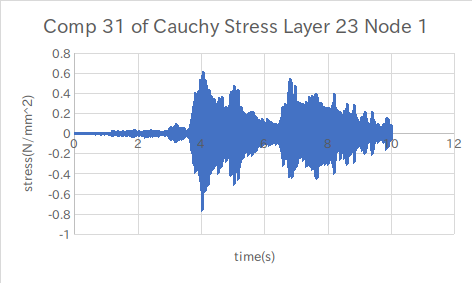
↑ZX方向?の応力(圧縮)

ZX方向の応力が予想と近いグラフとなった。
・Marcでは応力の33が橋軸の方向(Z軸)となるらしい。
・どの方向の応力を確認するべきか・「stress31」は本当にZX方向であると言えるのかこれについては今後マニュアルなどを読み検討していく必要がある。

↑

中実断面†

収束判定などをより詳細に設定し解析を行った。

桁部分はSM400材と仮定しており、ヤング率は200GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。
断面が100mm×100mmの長さ1000mmの部材では揺れが小さかったため、50mm×10mm、長さ1000mmの部材にした。
ケーブル部分は平行線ケーブルPWSと仮定しており、ヤング率は195GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。線膨張係数は1.25e-5である。
ケーブルの直径は8mmであり、桁の固定端から高さ1000mmの位置に固定している。回転自由である。
節点温度を-200℃とし、ケーブルプレストレスを導入する。
SM400、PWSそれぞれに応力-ひずみ関係（構成則）を適用し、非線形解析とした。
固定端に兵庫県南部地震の変位を入力した。

ケーブル腐食の再現は断面積の減少によって再現した。
下の表にケーブル腐食時の断面積と直径をまとめる。

Model	Area reduction rate	Area	Diameter
ModelA	0%(健全時)	50.27	8
ModelB	30%	35.15	6.69
ModelC	50%	25.16	5.66

〇結果

↑先端部分の相対変位

↑桁基部の応力

↑ケーブル応力

	disp	stress	tensile stress
A&B	1.12	1.02	1.40
A&C	1.29	1.06	1.96

各応答値の増加→ケーブル腐食の影響を確認することができた。

↑

薄肉断面†

桁部分はSM400材と仮定しており、ヤング率は200GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。
桁部分は50mm×10mm、厚さ2㎜、長さ1000mmの部材にした。
ケーブル部分は平行線ケーブルPWSと仮定しており、ヤング率は195GPa、ポアソン比0.3、密度は7.9e-9(ton/mm^3)としている。線膨張係数は1.25e-5である。
ケーブルの直径は8mmであり、桁の固定端から高さ1000mmの位置に固定している。回転自由である。
節点温度を-200℃とし、ケーブルプレストレスを導入する。
SM400、PWSそれぞれに応力-ひずみ関係（構成則）を適用し、非線形解析とした。
固定端に兵庫県南部地震の変位を入力した。

ケーブル腐食の再現は断面積の減少によって再現した。

〇結果

↑先端部分の相対変位

↑桁基部の応力

↑ケーブル応力

	disp	stress	tensile stress
A&C	1.18	1.28	2.74

各応答値の増加→ケーブル腐食の影響を確認することができた。
また、薄肉断面ではケーブル応力の増加が中実断面よりも大きくなった。

↑

課題†

1.解析のtime stepを一定にする
2.ケーブル部分の要素(引張力のみを持つように)

1.について
時刻歴応答解析における地震動の区間線形化の影響
・解析の計算ステップをサンプリング間隔より小さくする場合、区間線形保管が一般的。
・地震波が時間軸上の離散加点で折れ、その前後で直線的に変化するような部分線形関数であると考えるのは不自然。
→サンプリングデータに対して特に補正などはしていない
→現在の手法(Marcが自動で収束可能となる時間間隔で計算する(計算間隔が一定ではない)方法)ではサンプリング時刻ではない点で計算が不正確になっている可能性が高い。

2.について
No compressipn Materialmp記載がある。
引張と圧縮で材料定数（おそらくヤング率？）を変更、ある意味異方性のような設定があるらしい。どこでやるかは不明。

一般的には圧縮に対する剛性を極端に低くして再現を行うらしい。

Thickness Direction - Tension The tensile behavior of the gasket in the thickness direction is linear elastic and is governed by a tensile modulus.
The latter is defined as a pressure per unit closure distance (that is, length). can optionally be varied as a function
of temperature and spatial coordinates by using a multi-variate table

Some materials exhibit appreciably different behavior in compression from that in tension even in the small strain
range. For uniaxial loading the magnitude of the strain in that direction becomes the effective strain, i.e.,

The nonlinear elastic capability in MSC Nastran was designed to satisfy the equivalence of the deformation work per
unit volume in the simple tension to the strain energy per unit volume (conservation of energy), while the work done
for deformation may be defined by a stress-strain curve in simple tension, i.e.,

Some materials exhibit appreciably different behavior in compression from that in tension even in the small strain
range. For uniaxial loading the magnitude of the strain in that direction becomes the effective strain, i.e.,
for uniaxial tension in x
for uniaxial compression in x
In order to remain compatible with the MSC Nastran implementation of this material model, the user has the option
to ignore the uniaxial compression data, even if it is supplied on input.
In case of this unsymmetric material behavior, we need to be able to distinguish between a state of compression and a
state of tension. There are two known data points for one effective strain , namely the effective stress for uniaxial
tension and the effective stress for uniaxial compression . Some method of interpolation or extrapolation is
required to predict the effective stress for the general stress state using two known data points.
The first stress invariant has been adopted for interpolation/extrapolation as follows

To distinguish a tension or compression stress state the hydrostatic strain is computed.
If the hydrostatic strain is positive the total stresses are calculated based upon tensile properties. Resulting in and
If the hydrostatic strain is negative, the total stresses are calculated based upon compressive properties

↑

例題†

○土木振動工学　例題
「森北出版　土木振動学」の例題より

ばね定数k=1000t/mの柱で支持される
重量W=10tの一層ラーメンが地動加速度 
α=3000ωt mm/s^2(ω=20 rad/s) を受けるときの
ラーメンの相対変位が5.15(mm)である.

〇Marcでモデルを作成。

↑解析モデル

モデル諸元・質点部分
(x,y,z)=(1000,10,10)
ヤング率200GPa、密度1e-5(t/mm^3)
・橋脚部分
(x,y,z)=(20,300,20)
ヤング率はE=kl^3/24I より
8.4375e+2GPa

〇解析結果

↑橋脚部分の変位

↑ラーメン左端の絶対変位

↑相対変位

相対変位の最大値は5.077
例題の値との相対誤差は-1%

→Marcでは解法が妥当であると言える

↑

Marc_mentant　連鎖崩壊†

↑

斜張橋モデル†

橋長：540m，中央支間：300m，側径間：120m
主桁：sm400（降伏応力：235MPa），主塔：sm490(降伏応力：315MPa)，ケーブル：ST1570（第１降伏点：1160MPa，第２降伏点：1570MPa）
ケーブル，主径間：左右それぞれ７本(left:C7-C13,right:C14-C20)，側径間：左右それぞれ６本(left:C1-C6,right:C20-C26)
ケーブルの直径

cable C1 C2C3 C4C5 C6C7 C8-C10 C11-C13

D(m) 0.150 0.127 0.122 0.085 0.121 0.124
主桁，主塔断面

境界条件
主桁：両端および主塔横梁部で橋軸方向のみ自由
主塔：完全固定

↑

応力-ひずみ関係†

ケーブルの腐食を応力-ひずみ関係によって再現した．

↑

C1（アンカーケーブル）破断†

主桁スパン中央部の橋軸鉛直方向(y方向)変位

ケーブル応力（側径間）

ケーブル応力（中央径間）

ケーブルの塑性ひずみ（側径間）

ケーブルの塑性ひずみ（中央径間）

主桁の応力（C3とC4の中間地点）

ケーブルの破断時刻

↑

C13（センターケーブル）破断†

主桁スパン中央部の橋軸鉛直方向(y方向)変位

ケーブル応力（左側側径間）

ケーブル応力（左側中央径間）

ケーブル応力（右側中央径間）

ケーブル応力（右側側径間）

ケーブルの塑性ひずみ（左側側径間）

ケーブルの塑性ひずみ（左側中央径間）

ケーブルの塑性ひずみ（右側中央径間）

ケーブルの塑性ひずみ（右側側径間）

主桁の応力(C10付近，C9-C10間)

ケーブルの破断時刻

時刻250.01sでC13が破断
→時刻251.31sでC11が破断
→時刻251.39sでC12が破断
→時刻251.55sでC10が破断
→時刻251.66sでC9が破断
→時刻251.75sでC8が破断
→時刻251.87sでC7が破断
→時刻252.15sでC14が破断
→時刻252.21でC16が破断，C10付近（C9-C10間）に塑性ヒンジが形成され全体崩壊

↑

破断ケーブルの関係†

破断ケーブル	連鎖崩壊	塑性ヒンジ箇所
C1	連鎖崩壊発生	C3付近
C2	連鎖崩壊発生	C3付近
C3	連鎖崩壊発生	C3付近
C4	連鎖崩壊発生	C3付近
C5	連鎖崩壊発生	C3付近
C6	連鎖崩壊しない	×
C7	連鎖崩壊しない	×
C8	連鎖崩壊しない	×
C9	連鎖崩壊しない	×
C10	連鎖崩壊しない	×
C11	連鎖崩壊発生	C10付近
C12	連鎖崩壊発生	C10付近
C13	連鎖崩壊発生	C10付近

↑

本解析モデルの課題，当面の課題†

→DAFの計算時に必要な破断ケーブルを除いたモデルの静的解析について
→側径間のケーブルが降伏応力を大きく上回る
→腐食時に関して（60%），側径間のケーブル本数を7本から6本に変更した際に，側径間はケーブル１本無い場合，冗長性に欠ける???

解決策提案
→・腐食度合を減らす
　・断面照査をやり直し（現段階で，腐食時に断面照査してないし，しなさいという基準もないが）

↑

断面積減少†

ケーブルの腐食を断面積の減少によって再現した．
断面減少率γが0%を健全時とし，30%，60%としたモデルを解析した

↑

C1破断時†

主桁スパン中央部の橋軸鉛直方向(y方向)変位

変位が急激に増加している．→崩壊している可能性が高い

ケーブル応力(側径間)

ケーブルの塑性ひずみ(側径間)

ケーブルに関して，C2,C3,C4,C5,C6の順番で破断している

主桁スパン中央部の応力応答

主桁スパン中央部はt=251.86sにて全断面降伏している

時刻250sでC1が破断
→時刻251.75sでC2が破断
→時刻251.86sでC3が破断，同時に主桁スパン中央部に塑性ヒンジが形成（全断面降伏）され，全体崩壊

↑

減衰値比較†

減衰定数の変化により連鎖崩壊にどのような影響があるか．
減衰値0%，0.5%，1%，2%で比較

C2の応力

降伏応力に到達する時刻の差

0%	0.5%	1%	2%
0	0.2	0.2	0.2

C2の塑性ひずみ

破断ひずみに到達する時刻の差

0%	0.5%	1%	2%
0	0.1	0.12	0.13

C3の応力

降伏応力に到達する時刻の差

0%	0.5%	1%	2%
0	0.6	0.24	0.27

C3の塑性ひずみ

破断ひずみに到達する時刻の差

0%	0.5%	1%	2%
0	0.25	0.27	0.27

主桁スパン中央，橋軸鉛直方向変位

0%と減衰有では差が大きいが減衰値の大きさによる差はほとんどない

主桁応力分布（中立軸）

0.5%の応力分布のみやや位置が違う
→他のデータも0.1s後にはその位置が降伏
→誤差だと判断

橋梁モデル崩壊過程

崩壊（塑性ヒンジ形成）時間の差

0%	0.5%	1%	2%
0s	0.17s	0.21s	0.17s

ケーブルの破断に関して，減衰値の大きさの違いによる影響が有．
しかし，モデル橋全体の崩壊時刻に関して，減衰値の大きさの違いによってそこまで大きな影響はない．

↑

marcメモ†

INFO: Analysis dimension is derived from geometric property type Structural 3-D Solid Section Beam.

INFO: Assuming 3-D analysis!

ERROR: Job job1:
Found 50 element(s) with an element type that is incompatible
with the type (Structural 3-D Solid Section Beam) of the assigned geometric property!

INFO: Found 1 error and 0 warnings.

marc エラーコード
https://help.hexagonmi.com/bundle/marc_2020/page/combined_book/volc/cappa/TOC.Exit.Numbers.1001.2000.xhtml

↑

弾性域のひずみ†

色々試してみたが，「comp33 of elasticstrain layer1」が一番与えた応力ーひずみ関係と近い結果を得ることができる．
なぜ完全に一致しないかはまだわかっていない．
塑性域は「全相当塑性ひずみ」で完全一致する．

↑

終了番号†

3011 モデルが塑性破壊
2004 剛体変位

↑

salome_meca†

↑

梁要素†

↑

現段階での問題点，課題†

曲げモーメントの出力できない．応力もできない?軸力は可能でけれども手計算と一致しない
現時点でケーブルはトラス要素を用いている．おそらく圧縮力が発生する．
非線形解析と動的解析を組み合わせた解析がまだ１回も回ったことがない．できるらしいが
動的の精度の問題

↑

梁要素の簡易モデルの地震解析†

MONO_APUIとMULT_APUIではやり方が少し違う
○現段階でわかっていること
1.MODE_STACを使用する
2.地震荷重（CALC_CHAR_SEIS）を支点の数だけ作る
3.DYNA_BIBRAのLoadのところに支点の数だけ荷重を適用する

１自由度系の理論値とsalomeの計算は一致しなかった。~
自分に耐震工学の知識がないため理論値があっているのかわからない。~
文献、論文などを読みつつマークとを比較していく。~

マークで解析した.(x,y,z=10,10,1000)固定端に変位を与えるやり方。~
このやり方が解析方法として正しいか検討する必要有~

salomeの結果とmarcの結果が大幅に違う.(x,y,z=10,10,1000)~
片持ち梁で一致させる.~

○課題
1.CAD、マークと一致させる
→秋山　max:0.6 min-0.6 CAD max:0.4 min:0.35
→固有振動数は一致している。
→マークもあいていれば使用していきたい。。。
2.応力、モーメントの出力
→現段階では変位、速度、加速度しか出力できていない
→code_asterのマニュアルでは応力は出力できそう。モーメント、、、、

↑

梁要素の片持ちばりの地震解析†

シェル要素では板厚を考慮できない。(考慮した地震解析の方法は不明)
→同条件で梁要素で地震解析(梁要素もAFEE_〜で半径を設定する)

また、青木先生にCADで解析してもらったものを青色のグラフに示す。

・半径5mm

・半径50mm

CADは東西、南北、上下の三方向合成の加速度を使用。
salomeは最大加速度（東西）を使用。
そのため完璧には一致しないがグラフは一致していると言える。

→梁要素であれば断面の特性を反映可能

→梁要素で地震解析を進めていく

→梁要素の線形解析へ^

↑

断面定数の算出(薄肉断面梁)†

・salome2019を用いて断面定数を算出する。
○ジオメトリー
・平面を用いて断面を作る
・外側の四辺、内側の四辺、外側の四辺上の角の点、内側の四辺上の角の点、この4つのグループを作る。
○メッシュ
・メッシュを作成
・ジオメトリグループの作成
・メッシュをmedファイルでエクスポート
○aster_study
・メッシュ適用・Model Definition > MACR_CARA_POUTRE >「GROUP_MA_BORD」を外の辺に > 「GROUP_NO」を外の点に > メッシュを適用
・Model Definition > MACR_CARA_POUTRE　にて内側も同様に
・set output result で Formatをresultに、ファイル名を「kekka.resu」のようにする。
○計算を回してresultファイルを見る。

↑

シェル要素†

100☓100☓1000の箱桁をシェル要素で減衰無しで地震をかける（2ヶ月苦戦中）

func = DEFI_FONCTION(
 NOM_PARA='INST', 
 NOM_RESU='accel', 
 VALE=(0.0, 0.0, 0.01, 5712.270737, 0.02, 5725.383759, 0.03, 5726.099014, 0.04, 5717.039108, 0.05, 5706.071854, 0.06, 5727.767944, 0.07, 5738.019943,0.08, 5732.774734, 0.09, 5733.48999, ...)
 ) # sequences have been limited to the first 20 occurrences.

listr = DEFI_LIST_REEL(
 DEBUT=0.0, 
 INTERVALLE=_F(
   JUSQU_A=10.0, 
   PAS=0.01
 )
)

func0 = CALC_FONCTION(
 COMB=_F(
   COEF=1.47, 
   FONCTION=func
 )
)

oad0 = AFFE_CHAR_MECA(
 DDL_IMPO=_F(
   GROUP_MA=('kotei', ), 
   LIAISON='ENCASTRE'
 ), 
 MODELE=model
)

ASSEMBLAGE(
 CARA_ELEM=elemprop, 
 CHAM_MATER=fieldmat, 
 CHARGE=(load0, ), 
 MATR_ASSE=(_F(
     MATRICE=CO('mass'), 
     OPTION='MASS_MECA'
   ), _F(
     MATRICE=CO('Rigi'), 
     OPTION='RIGI_MECA'
   )), 
 MODELE=model, 
 NUME_DDL=CO('nddl'), 
 VECT_ASSE=_F(
   CHARGE=(load0, ), 
   OPTION='CHAR_MECA', 
   VECTEUR=CO('Vect')
 )
)

field = CALC_CHAR_SEISME(
 DIRECTION=(1.0, 0.0, 0.0), 
 MATR_MASS=mass, 
 MONO_APPUI='OUI'
)

modes0 = CALC_MODES(
 CALC_FREQ=_F(
   NMAX_FREQ=10
 ), 
 MATR_MASS=mass, 
 MATR_RIGI=Rigi, 
 OPTION='PLUS_PETITE', 
 VERI_MODE=_F(
   STOP_ERREUR='NON'
 )
)

PROJ_BASE(
 BASE=modes0, 
 MATR_ASSE_GENE=(_F(
     MATRICE=CO('massgene'), 
     MATR_ASSE=mass
   ), _F(
     MATRICE=CO('rigigene'), 
     MATR_ASSE=Rigi
   )), 
 STOCKAGE='DIAG', 
 VECT_ASSE_GENE=_F(
   TYPE_VECT='FORC', 
   VECTEUR=CO('vectgene'), 
   VECT_ASSE=field
 )
)

resharm = DYNA_VIBRA(
 BASE_CALCUL='GENE', 
 ETAT_INIT=_F(
   DEPL=vectgene, 
   VITE=vectgene
 ), 
 EXCIT=_F(
   ACCE=func, 
   DEPL=func0, 
   VECT_ASSE_GENE=vectgene, 
   VITE=func0
 ), 
 INCREMENT=_F(
   LIST_INST=listr
 ), 
 MATR_MASS=massgene, 
 MATR_RIGI=rigigene, 
 MODE_CORR=modes0, 
 SCHEMA_TEMPS=_F(
   SCHEMA='NEWMARK'
 ), 
 TRAITEMENT_NONL='IMPLICITE', 
 TYPE_CALCUL='TRAN', 
 VITESSE_VARIABLE='NON'
)

restran = REST_GENE_PHYS(
 CRITERE='RELATIF', 
 LIST_INST=listr, 
 NOM_CHAM=('ACCE', 'DEPL', 'VITE'), 
 NUME_DDL=nddl, 
 PRECISION=1e-06, 
 RESU_GENE=resharm
)

 IMPR_RESU(
 FORMAT='MED', 
 RESU=(_F(
     CARA_ELEM=elemprop, 
     NOM_CHAM=('DEPL', ), 
     RESULTAT=modes0
   ), _F(
     CARA_ELEM=elemprop, 
     LIST_INST=listr, 
     NOM_CHAM=('ACCE', 'VITE', 'DEPL'), 
     RESULTAT=restran
   )), 
 UNITE=80
)

○結果シェルの厚さ6mm

シェルの厚さ20mm

地震のような挙動は示している。
しかしシェルの厚さが変化しているにもかかわらず変位に変化がない。
これはおかしい。

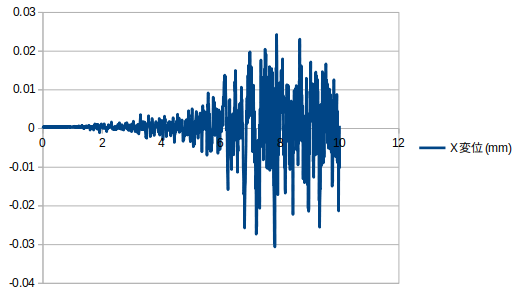
青木先生がキャドで解析してくれたもの
挙動は比較的同じだが値が違う
シェル要素の厚さ（断面特性）を反映できていない

今使用しているDYNA_VIBRA（geneのtran）には
elemprop = AFFE_CARA_ELEM(シェル要素の断面の特性)を適用するコマンドがない
※GENE=モードベース（おそらくモード重ね合わせ法）
　PHYS=物理計算ベース？
　harm=定常波
　tran=非定常波
code_aster(DYNA_VIBRA等)にも特にシェル要素に関する記述はない
シェルではできない？→→そんなことあります？

↑

秋山の簡易モデルに地震をかけてみる†

計算回った。

しかし、スケールファクター大きくしないと変形しない。（これは60万倍）
→修正。 →シェル要素だけでやってみる。

↑

線形解析†

Exception user raised but not interceptee.                !
  ! The bases are fermees.                                        !
  ! Type of the exception: error                                  !
  !                                                               !
  !  the computation of the option:  CARA_SECT_POUT3              !
  !  is not possible for any the types of elements of the LIGREL. !

このエラーは結合する線を「Assign finite element」「AFFE_CARA_ELEM」に「Assign a material」に含めないと出てくる。

↑

梁要素の線形解析†

桁部分が(X,Y,Z)=(100,100,1000)、ケーブルをY軸方向に1000mmのところに固定した簡易モデルを全て梁要素で作る。
ケーブル部分はセグメント数を1にする。

○メッシュの切り方
・ジオメトリーで全て結合（フューズ）してしまう。
→グループの作成で「桁」「ケーブル」を作成
→モデル全体に対してメッシュを作成し、セグメント数を1にする
→桁に対してサブメッシュを作成する

この方法で作成したモデルの先端部分に鉛直荷重1kNを載荷した。
温度変化(-200℃)でプレストレスを与えた
○結果
マーク:3.580mm salome:3.492mm →ピンになっている

↑

結合の問題†

プレストレスをかけることに成功したが、変形が食パンのような形になっていておかしい。
→結合する場所を端から少しずらした。

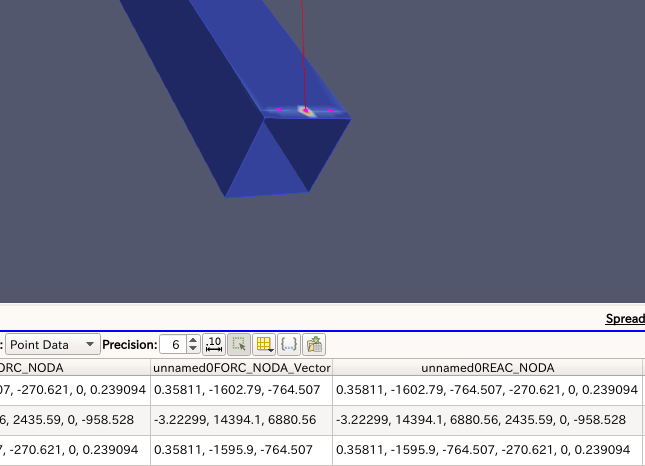
しかし、食パン型は直らず、結合してる線に沿ってリアクション（節点反力）が発生してる。
→違う結合方法の模索が必要

・メッシュを切ってからノードを作り、エッジを作成した。
→結合しないようだ。~

・LIAISON_ELEでケーブルと桁を結合しているが、剛結になっていると思われる。
「LIAISO_UNIF」というものがノードの自由度を同じにできるらしい

→やってみたところ、変形の形もよく、結合箇所のDRXのREAC_NODA(節点反力)は発生しなかった。

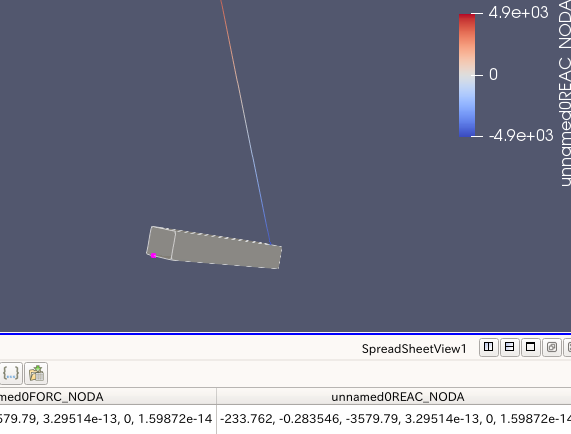
→しかし載荷しているにもかかわらず、根元部分にはDRXのREAC_NODAは発生していない。
→REAC_NODAのDRXがモーメントと思っていたが違う可能性がある。

↑

ピン接合†

梁要素にPOU_D_E（節点に回転を許さない）ではなく、BARREを適用（節点に回転を許す）
→境界条件で固定端をDX-=0,DY=0,DZ=0とした。(DRX=0とかとするとエラーが発生する。)
→変位がより大きくなった。
→これはなぜか？ヒンジになっているのか？

○BARRE要素（トラス要素）での解析結果

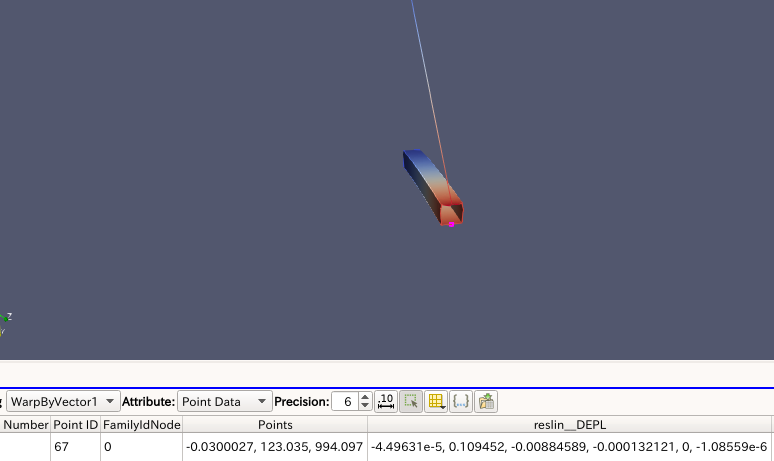
→プレストレスがかかってない
→次の方法でプレストレスをかける

tensyon = CREA_CHAMP(
 AFFE=_F(
   NOM_CMP=('TEMP', ), 
   TOUT='OUI', 
   VALE=(-200.0, )
 ), 
 MODELE=model, 
 OPERATION='AFFE', 
 TYPE_CHAM='NOEU_TEMP_R'
)

 AFFE=(_F(
     GROUP_MA=('ketsusen', 'keta'), 
     MATER=(materK, )
   ), _F(
     GROUP_MA=('hari', ), 
     MATER=(materH, )
   )), 
 AFFE_VARC=_F(
   CHAM_GD=tensyon, 
   GROUP_MA=('hari', ), 
   NOM_VARC='TEMP', 
   VALE_REF=0.0
 ), 
 MAILLAGE=mesh, 
 MODELE=model
 )

プレストレスがかかり、上方向にたわんだ。

・やろうとしたこと 1 liaiso_ddl

↑

簡易モデルの作成†

(x,y,z)=(100,100,1000)の簡易モデルをケーブルを梁要素で、桁をシェル要素で作成。
→梁要素、シェル要素ともに応力、ひずみが計算できないため、試行錯誤中
→シェル要素の応力、ひずみの計算、出力に成功
・梁要素は絶賛試行錯誤中
→梁は軸力(FORCE)を見ることができたため、OK

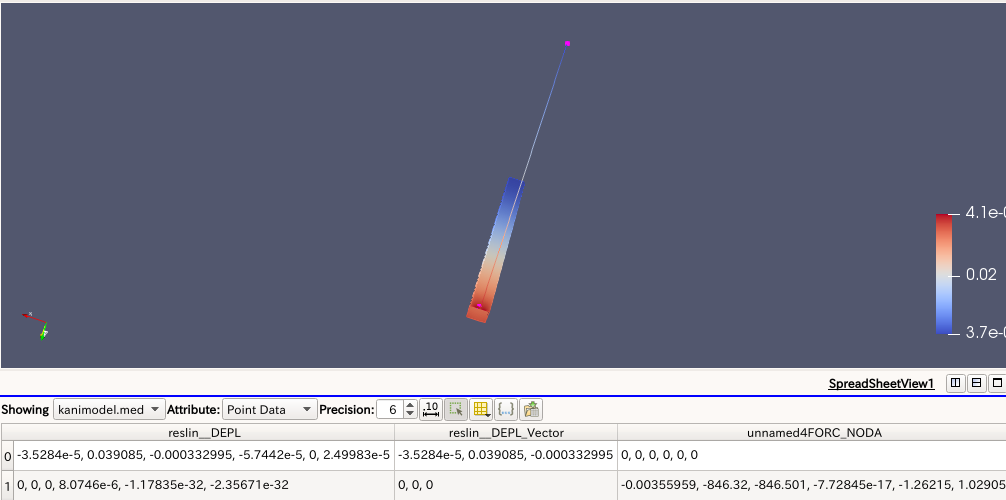
しかし、変位が角田さん&梅宮くんのと異なる(符号が違う)

→剛結になっている?
→ピン接合にしたい。

↑

salomemeメモ†

↑

salome参考資料†

↑

梁要素メモ†

ジオメトリーでフューズしても、「liaison_solide」で結合しても剛体になる。

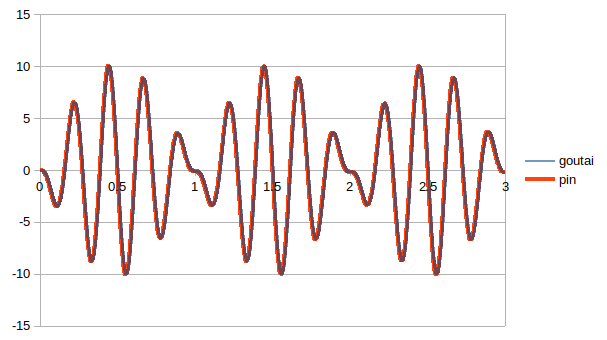
グラフは完全一致している
pinはピンになっていない。^
どっかに梁要素はフューズするとピンになると書いていたがそんなことない。

↑

シェル要素メモ†

・以下の方法でシェル要素の応力を計算、出力可能

unnamed1 = CALC_CHAMP(
 CARA_ELEM=elemprop, 
 CHAM_MATER=fieldmat, 
 CONTRAINTE=('SIGM_ELNO', ), 
 DEFORMATION=('EPSI_ELNO', ), 
 GROUP_MA=('keta', ), 
 MODELE=model, 
 RESULTAT=reslin)

unnamed2 = POST_CHAMP(
 EXTR_COQUE=_F(
   NIVE_COUCHE='SUP', 
   NOM_CHAM=('EPSI_ELNO', 'SIGM_ELNO'), 
   NUME_COUCHE=1
 ), 
 GROUP_MA=('keta', ), 
 RESULTAT=unnamed1)

unnamed3 = CALC_CHAMP(
 CARA_ELEM=elemprop, 
 CHAM_MATER=fieldmat, 
 CONTRAINTE=('SIGM_NOEU', ), 
 DEFORMATION=('EPSI_NOEU', ), 
 GROUP_MA=('keta', ), 
 MODELE=model, 
 RESULTAT=unnamed2)

output

IMPR_RESU(
 FORMAT='MED', 
 RESU=(_F(
     CARA_ELEM=elemprop, 
     NOM_CHAM=('DEPL', ), 
     RESULTAT=reslin, 
     TOUT='OUI'
   ), _F(
     CARA_ELEM=elemprop, 
     NOM_CHAM=('FORC_NODA', 'REAC_NODA'), 
     RESULTAT=unnamed4
   ), _F(
     CARA_ELEM=elemprop, 
     GROUP_MA=('keta', ), 
     NOM_CHAM=('EPSI_NOEU', 'SIGM_NOEU'), 
     RESULTAT=unnamed3
   )), 
 UNITE=2
   )

↑

参考資料†

↑

参考文献†

ケーブル腐食を考慮した斜張橋の終局強度および疲労寿命
構造工学論文集 Vol. 67A (2021 年 3 月)
中村俊一、青木由香利

・斜張橋においてケーブルは重要な役割を果たす。
・ケーブルが腐食すると、じん性、耐力、疲労強度が低下し、断面積が減少する。
・異なるスパン長のモデルで、腐食（断面積の減少）の影響、ケーブルの疲労寿命を求める。
・断面積の減少に比例して終局強度は低下する。
・ケーブルの伸びが1%（健全時の伸びは4%）まで低下すると終局強度は小さくなる。
・ケーブルの腐食が進行するとともに疲労寿命は小さくなり、断面積の減少を考慮すると疲労寿命は著しく低下する。

橋梁用ケーブルの最近の話題と展望
土木学会論文集 No.444/VI-16,pp97-106,1992.3
三田村武　中居博　渡邊英一　杉井謙一

台湾南方澳橋，NEWS
吊橋ケーブルの腐食機構に関する研究
土木学会論文集 No.637
古家和彦、北川信、中村俊一、鈴村恵太、聖生守雄

鋼構造委員会出版物斜張橋設計~

平成7年兵庫県南部地震と構造物の被害の概要
川田技報　Vol15 1996
越後滋　米田昌弘　片岡章悟　磯光夫

振動計測から推定される斜張橋ケーブルの振動特性
第37回土木学会関東支部技術研究発表会
中央大学矢口繁　中央大学佐藤尚次　平野廣和
雪沢大橋ケーブル破断への対応と今後の維持管理について
神田隆仁　船木孝仁　高橋昌平　高野優　越前谷宏昭

長大斜張橋の想定大規模地震時の非線形挙動に関する研究
土木学会構造工学論文集 Vol.53A(2007 年 3 月)
和崎宏一　柳野和也　廣住敦士　野中哲也

第ⅴ編　吊橋主ケーブルの腐食
鋼橋技術研究会

土木研究所資料　過去の大規模地震における落橋事例とその分析

大規模地震時における長大吊橋の終局限界状態に関する解析的研究構造工学論文集 Vol.55A ( 2009 年 3 月) 遠藤和男　福永勧　家村浩和　八田政仁　野中哲也

「鋼斜張橋モデルの地震時応答解析と実測データの比較」
土木学会地震工学論文集（2007 年 8 月）
宮森保紀　池田憲俊　木村浩　三上修一　大島俊之

大規模計算による長大橋地震応答解析の構造要素モデルの高度化に関する検討
土木学会論文集 A2(応用力学), Vol. 73, No. 2 (応用力学論文集 Vol. 20), I_769-I_780, 2017.
八ツ元仁馬越一也金治英貞中村真貴野中哲也

実吊橋主ケーブルの腐食調査におけるさび組成分析に基づく腐食評価基準の検討
構造工学論文集 Vol. 66A (2020 年 3 月)
木下幸治　矢野義知　畑佐陽祐　蓮池里菜　宮地一裕

「連鎖的な部材破壊を考慮した鋼橋のリダンダンシー解析法の提案」
構造工学論文集 Vol.56A ( 2010 年 3 月)
野中哲也宇佐美勉岩村真樹廣住敦士吉野廣一

長大斜張橋における 2018 年大阪府北部地震の地震観測記録と応答特性の評価
土木学会論文集A1（構造・地震工学）, Vol. 75, No. 4（地震工学論文集第38巻）, I_433-I_442, 2019.
馬越一也中村真貴服部匡洋大石秀雄篠原聖二

振動測定データに基づいた鋼斜張橋モデルの非線形地震時応答解析
土木学会構造工学論文集 Vol.55A（2009 年 3 月）
木村浩士　宮森保紀　三上修一　大島俊之

鋼斜張橋モデルの地震時応答解析と実測データの比較
土木学会地震工学論文集（2007 年 8 月）
宮森保紀　池田憲俊　木村浩士　三上修一　大島俊之

大規模地震動に対する鋼斜張橋全体系の非線形動的解析（その2）
第2回地震時保有耐力法に基づく橋梁の耐震設計に関するシンポジウム講演論文集(1998年12月)
吉澤　努　川神　雅秀

鋼斜張橋(荒津大橋)の飛散型地震応答解析とモデル化の検討
第2回地震時保有耐力法に基づく橋梁の耐震設計に関するシンポジウム講演論文集(1998年12月)
大塚久哲　堂上幸男　山平喜一郎　加藤一郎　藤野明義

長大鋼斜張橋の橋軸方向地震応答に対する簡易照査法
土木学会論文集No.658/VI-48,193-205,2000.9
米田昌弘　西澤毅

横浜ベイブリッジの耐震補強設計における鋼上部構造を対象とした性能照査
土木学会論文集Ａ Vol.66 No.1,13-30,2010.1
山本泰幹　半野久光　藤野陽三　矢部正明

長大斜張橋における 2018 年大阪府北部地震の地震観測記録と応答特性の評価
土木学会論文集A1（構造・地震工学）, Vol.75,No.4（地震工学論文集第38巻）,I_433-I_442,2019
馬越一也　中村真貴　服部匡洋　大石秀雄　篠原聖二

強震記録に基づく斜張橋の振動特性
地震工学研究発表会講演概要,19巻(1987)
川島一彦　運上茂樹　吾田洋一

「コンクリート斜張橋の地震時挙動に関する解析的研究」
地震工学研究発表会講演概要,19巻(1987)
横山正義　田中茂義　岩野政浩　丸山昭義

↑

耐震工学参考資料†

・芝浦工業大学　地震防災学　資料
　 http://www.eq.db.shibaura-it.ac.jp/lecture/taishin/01/taishin_01.pdf
　 http://www.eq.db.shibaura-it.ac.jp/lecture/taishin/02/taishin_02.pdf
・工学院大学　地震工学　資料（防災チック）
　 http://kouzou.cc.kogakuin.ac.jp/Open/%E5%9C%B0%E9%9C%87%E5%B7%A5%E5%AD%A6%E8%B3%87%E6%96%99/
・千葉大学　振動工学
　 https://shake.tu.chiba-u.ac.jp/lecture/vibration/
・武蔵工業大学　振動工学基礎
　 http://c-pc8.civil.tcu.ac.jp/RC/ciber/tai/tai_pdf/01_shindo-base.pdf
・地震解析のメモ
　 https://www.jaee.gr.jp/jp/wp-content/uploads/2012/02/kaishi03.pdf

・線形の動的における減衰のモデル by code_aster
　 https://www.code-aster.org/V2/doc/default/en/man_r/r5/r5.05.04.pdf
・東北地方太平洋沖地震の余震観測記録に基づいた鶴見つばさ橋の動特性の検証
　 https://www.jstage.jst.go.jp/article/jscejseee/73/4/73_I_730/_pdf/-char/ja
・知っておきたい振動解析
　 https://www.structure.jp/column36/column36_1.html
・建築分野　構造設計学Ⅲ
　 https://archi.hiro.kindai.ac.jp/lecdocument/kozosekkei3/30p.pdf
・減衰について
　 https://www.bakko-hakase.com/entry/218_C-H
・減衰について
　 https://www.kozosoft.co.jp/gijyutu/s18.html
・周波数積分
　 https://www.onosokki.co.jp/HP-WK/c_support/faq/cf5200/CF5200_integlation.htm
・地震発生のメカニズム
　 https://www.bousai.metro.tokyo.lg.jp/bousai/1000929/1000305.html
・兵庫県南部地震・第２次提言
　 https://www.jsce.or.jp/committee/earth/chap1.html~　

↑

salome_meca 及川さんからいただいたデータ†

・mesh、model definitionは今までどおり
・material

mater = DEFI_MATERIAU(
 ELAS=_F(
   AMOR_ALPHA=0.03, 
   E=7500.0, 
   NU=0.4, 
   RHO=3.8e-10
 )
)

mater0 = DEFI_MATERIAU(
 ELAS=_F(
   E=10000.0, 
   NU=0.3, 
   RHO=1e-09
 )
)

fieldmat = AFFE_MATERIAU(
 AFFE=(_F(
     GROUP_MA=('Box_2', 'translation_2', 'translation_3', 'Box_3'), 
     MATER=(mater, )
   ), _F(
     GROUP_MA=('translation_1', 'Box_1'), 
     MATER=(mater0, )
   )), 
 MAILLAGE=mesh, 
 MODELE=model
)

・functions and lists

func4 = DEFI_FONCTION(
 NOM_PARA='INST', 
 NOM_RESU='acce', 
 VALE=(0.0, 0.0, 0.02, 0.03, 0.04, 0.03, 0.06, 0.03, 0.08, 0.03, 0.1, 0.03, 0.12, 0.03, 0.14, 0.03, 0.16, 0.03, 0.18, 0.03, ...)
) # sequences have been limited to the first 20 occurrences.

func5 = CALC_FONCTION(
 COMB=_F(
   COEF=1.47, 
   FONCTION=func4
 )
)

listr = DEFI_LIST_REEL(
 DEBUT=0.0, 
 INTERVALLE=_F(
   JUSQU_A=30.0, 
   PAS=0.02
 )
)

・BC and Loads

load = AFFE_CHAR_MECA(
 DDL_IMPO=_F(
   DX=0.0, 
   DY=0.0, 
   DZ=0.0, 
   GROUP_MA=('kotei', )
 ), 
 MODELE=model
)

・pre alalysis

ASSEMBLAGE(
 CHAM_MATER=fieldmat, 
 CHARGE=(load, ), 
 MATR_ASSE=(_F(
     MATRICE=CO('mass'), 
     OPTION='MASS_MECA'
   ), _F(
     MATRICE=CO('stifness'), 
     OPTION='RIGI_MECA'
   ), _F(
     MATRICE=CO('amo'), 
     OPTION='AMOR_MECA'
   )), 
 MODELE=model, 
 NUME_DDL=CO('nddl')
)

・BC and Loads

field = CALC_CHAR_SEISME(
 DIRECTION=(-1.0, 0.0, 0.0), 
 MATR_MASS=mass, 
 MONO_APPUI='OUI'
)

・analysis

modes = CALC_MODES(
 CALC_FREQ=_F(
   NMAX_FREQ=10
 ), 
 MATR_MASS=mass, 
 MATR_RIGI=stifness, 
 OPTION='PLUS_PETITE', 
 VERI_MODE=_F(
   STOP_ERREUR='NON'
 )
)

・pre analysis

PROJ_BASE(
 BASE=modes, 
 MATR_ASSE_GENE=(_F(
     MATRICE=CO('MASSGENE'), 
     MATR_ASSE=mass
   ), _F(
     MATRICE=CO('rigi'), 
     MATR_ASSE=stifness
   ), _F(
     MATRICE=CO('amo1'), 
     MATR_ASSE=amo
   )), 
 NB_VECT=10, 
 VECT_ASSE_GENE=_F(
   TYPE_VECT='ACCE', 
   VECTEUR=CO('vectgene'), 
   VECT_ASSE=field
 )
)

・ analysis

resharm = DYNA_VIBRA(
 BASE_CALCUL='GENE', 
 EXCIT=_F(
   ACCE=func4, 
   DEPL=func4, 
   VECT_ASSE_GENE=vectgene, 
   VITE=func4
 ), 
 INCREMENT=_F(
   LIST_INST=listr
 ), 
 MATR_AMOR=amo1, 
 MATR_MASS=MASSGENE, 
 MATR_RIGI=rigi, 
 SCHEMA_TEMPS=_F(
   BETA=0.25, 
   GAMMA=0.5, 
   SCHEMA='NEWMARK'
 ), 
 TYPE_CALCUL='TRAN'
)

・post processig

restran = REST_GENE_PHYS(
 CRITERE='RELATIF', 
 LIST_INST=listr, 
 PRECISION=1e-06, 
 RESU_GENE=resharm, 
 TOUT_CHAM='OUI'
)

・out put

IMPR_RESU(
 FORMAT='MED', 
 RESU=(_F(
     NOM_CHAM=('DEPL', 'VITE'), 
     RESULTAT=restran
   ), _F(
     NOM_CHAM=('ACCE', ), 
     RESULTAT=modes
   )), 
 UNITE=80
)

↑

メモ†

↑

東北支部†

テーマ：吊形式構造物に対する基礎的地震応答解析
概要：2019年10月、台湾の南方澳大橋が崩壊する事故が発生した。原因の一つとしてケーブルの腐食が考えられている。
しかし、地震大国である日本では耐震性能が重要な意味を持つ。
本研究室ではケーブル腐食が斜張橋の終局強度に及ぼす影響に関する研究が進められている。そこで本研究では斜張橋を対象にケーブル腐食が地震荷重に対してどのような影響を及ぼすかを数値解析していく。
今回はその前段階であるケーブルを有する鋼構造物をモデルで作成し、地震荷重に対してケーブル腐食が影響を及ぼすかを確認する。

↑

土木学会全国大会†

ケーブル腐食を考慮した斜張橋モデルの地震応答解析
概要：斜張橋などの吊形式橋梁において，ケーブルは非常に重要な役割を担っている．近年，吊形式橋梁のケーブル腐食の事例が数多く存在している．
現在ケーブル腐食が斜張橋全体の終局強度への影響は明らかになっているが，地震が発生した際にケーブル腐食が斜張橋全体にどのような影響を及ぼすかは明らかになっていない．
本研究では，斜張橋を対象とし，ケーブル腐食時に地震荷重が作用した場合，ケーブル腐食が橋梁全体にどのような影響を与えるかを数値解析的に検討した．
ケーブル腐食の度合いが大きくなると，主桁スパン中央の最大応力，主塔基部の曲げモーメントへの影響が顕著にみられた．
概要

↑

日記†

10月30日
終了番号1001番
タイイングの問題の可能性があったため，心当たりのある箇所を全て確認＆修正

→エラー，終了番号1001
支承部分を一つ追加する？

10月24日
model600の橋軸直角方向の地震解析がエラー
終了番号は1001

Connectivity exceeded at the node given in the message:
 
     "MORE THAN MAXNP JOINED TO NODE..."
 
during in-core assembly of elements. This aborts the program
at that point. If this occurs during a contact analysis, try
to activate single sided contact on the CONTACT option. This
can also occur if a contacted element has a user defined 
tying on the contacted patch or edge.
 
Otherwise Marc system error; consult
MSC Software analyst.

メッセージで指定されたノードで接続性が超過した：
 
     "ノードへの最大接続数を超えています..."
 
というメッセージで指定されたノードで接続性が超過しました。これはプログラムを中断させる
されます。接触解析中にこの現象が発生した場合は
CONTACTオプションで片面接触を有効にしてみてください。これは
この現象は、接触した要素にユーザー定義の 
タイイングがある場合にも発生することがあります。
 
それ以外の場合はマークシステムエラーです。
MSCソフトウェアのアナリストにご相談ください。

9月11日
全国の練習
イタリアの斜張橋崩壊的な記事あったから書いておく
https://www.enr.com/articles/45001-death-toll-approaches-40-in-collapse-of-cable-stayed-bridge-in-italy
9月5日
直角方向の地震解析，断面減少30%,60%のstress，momentのデータまとめ直しを明日．
今日は鉛直方向のデータのまとめ．

9月3日
パソコンが起動できなかった、何もできず

8月31日
model600鉛直方向の地震では解析がうまくいった
それ以外の方向はやはりどこかが接触しているのかもしれない^

8月30日
軸方向の地震解析はエラー
全国のスライドづくり

8月29日
・model600の主塔，主桁をつなぐばね要素を変位に関して軸方向以外すべて剛性を強くした
http://kentiku-kouzou.jp/struc-sosendanryoku.html
https://media.lne.st/contents/Seven-important-things-to-keep-in-mind-when-conducting-research
https://sato000000.net/graduate-student-not-suitable
8月28日
主塔断面を修正．断面照査終了
→地震解析エラー
終了番号1001
8月21日
・model600の断面照査終了
・地震解析してみたがエラー
→桁と塔の一番下のケーブル定着部の距離が90mもあるからこれを小さくして，新しくモデルを作る
以下エラーコード

Connectivity exceeded at the node given in the message:

    "MORE THAN MAXNP JOINED TO NODE..."
 
during in-core assembly of elements. This aborts the program
at that point. If this occurs during a contact analysis, try
to activate single sided contact on the CONTACT option. This
can also occur if a contacted element has a user defined 
tying on the contacted patch or edge.
 
Otherwise Marc system error; consult
MSC Software analyst.

・荷重スケール20倍にて，主塔が座屈しているように見て取れた
板厚の変更
→鰓ー
→主塔形状の変更をしようと思います

1	3.0365e-08
2	3.0372e-08
3	3.6659e-08
4	3.6659e-08
5	4.3269e-08
6	4.3329e-08
7	5.1289e-08
8	5.1300e-08
9	5.2535e-08
10	5.2550e-08

cable	C1	C2C3	C4C5	C6C7	C8-C10	C11-C13
D(m)	0.150	0.127	0.122	0.085	0.121	0.124

1	5.771+0	6.929-5	0
0	0	0	0

1	0	0	3.00-2
0	0	0	0

秋山の修論日誌 の履歴(No.106)

修論†

Marc_mentant 地震応答解析†

重力荷重・斜張橋モデル_ケーブル・分割(2mにつき1要素)†

断面2次モーメントを任意で与える†

地震応答解析（水平方向）†

斜張橋モデル_modal300{ケーブル・分割(2mにつき1要素)}†

線形解析†

モード解析_フィルター無し†

理論値と比較†

地震応答解析(ケーブル2mにつき1要素)†

モード解析†

斜張橋モデル_model300(ケーブル・1要素)†

断面照査†

断面積減少†

橋軸直角方向†

橋軸鉛直方向†

破断ひずみ（応力ひずみ関係）の減少†

橋軸水平方向†

橋軸鉛直方向†

異なる腐食の再現方法の比較†

水平方向，30%†

水平方向，60%†

鉛直方向，30%†

鉛直方向，60%†

減衰†

減衰の与え方†

減衰定数の選定†

地震メモ†

斜張橋モデル_model600†

断面照査†

地震解析†

簡易モデル†

中実断面†

薄肉断面†

課題†

例題†

Marc_mentant 連鎖崩壊†

斜張橋モデル†

応力-ひずみ関係†

C1（アンカーケーブル）破断†

C13（センターケーブル）破断†

破断ケーブルの関係†

本解析モデルの課題，当面の課題†

断面積減少†

C1破断時†

減衰値比較†

marcメモ†

弾性域のひずみ†

終了番号†

salome_meca†

梁要素†

現段階での問題点，課題†

梁要素の簡易モデルの地震解析†

梁要素の片持ちばりの地震解析†

断面定数の算出(薄肉断面梁)†

シェル要素†

秋山の簡易モデルに地震をかけてみる†

線形解析†

梁要素の線形解析†

結合の問題†

ピン接合†

簡易モデルの作成†

salomemeメモ†

salome参考資料†

梁要素メモ†

シェル要素メモ†

参考資料†

参考文献†

耐震工学参考資料†

salome_meca 及川さんからいただいたデータ†

メモ†

東北支部†

土木学会全国大会†

日記†

秋山の修論日誌の履歴(No.106)

Marc_mentant　地震応答解析†

Marc_mentant　連鎖崩壊†